Moment d'inertie d'une sphère homogène vide
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 18 Oct 2007, 17:11
par rifly01 » 18 Oct 2007, 17:11
Bonjour,
Je ne vois pas comment calculer le moment d'inertie d'une sphère homogène vide : En fait je ne vois pas la différence entre une sphère homogène pleine (dans les calculs) qui a pour moment d'inertie
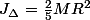
.
Merci d'avance,
 par Dominique Lefebvre » 18 Oct 2007, 17:52
par Dominique Lefebvre » 18 Oct 2007, 17:52
rifly01 a écrit:Bonjour,
Je ne vois pas comment calculer le moment d'inertie d'une sphère homogène vide : En fait je ne vois pas la différence entre une sphère homogène pleine (dans les calculs) qui a pour moment d'inertie

.
Merci d'avance,
c'est quoi une sphère vide??? Je te rappelle qu'une sphère est une surface! Le moment d'inertie que tu mentionnes est celui d'une boule de rayon r.
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 18 Oct 2007, 17:58
par rifly01 » 18 Oct 2007, 17:58
Ah,
Je voulais dire, par la sphère vide une coquille sphérique mince de rayon R.
(Une sphère plein dans ce cas est une boule).
 par Dominique Lefebvre » 18 Oct 2007, 18:09
par Dominique Lefebvre » 18 Oct 2007, 18:09
rifly01 a écrit:Ah,
Je voulais dire, par la sphère vide une coquille sphérique mince de rayon R.
(Une sphère plein dans ce cas est une boule).
"Sphère pleine" c'est un abus de langage... Si ton prof de géométrie différentielle ou de topo t'entendait!
Bref, le moment d'inertie d'une coquille sphérique est I =2/3mr^2 et celui d'une boule est I = 2/5mr^2
PS : j'ai oublié de préciser qu'il s'agit du moment d'inertie par rapport à l'axe de rotation... Important!
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 18 Oct 2007, 20:59
par rifly01 » 18 Oct 2007, 20:59
Re -
Comment vous faites pour retrouver ce résultat :
I =2/3mr^2 pour une coquille sphérique.
Je ne sais pas poser le calcul.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 18 Oct 2007, 21:18
par Skullkid » 18 Oct 2007, 21:18
Bonsoir, le calcul se fait sur le même principe que pour le moment d'une boule homogène par rapport à un axe qui passe par son centre, sauf qu'ici il faut intégrer sur la sphère (intégrale double) et non sur une boule.
L'aire d'une sphère de rayon R étant égale à
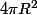
, la masse surfacique de la sphère est
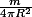
. A partir de là il n'y a plus à intégrer en coordonnées sphériques :
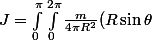^2 R d\theta R\sin\theta d\varphi=\frac{m}{4\pi R^2}\times R^4\times \frac43 \times 2\pi=\frac23 mR^2)
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 19 Oct 2007, 19:03
par flaja » 19 Oct 2007, 19:03
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
.