bonjour,
Une particule est notamment décrite par sa position et son impulsion .or, la probabilité de trouver une particule libre dans un élément de volume de lespace
des positions et des impulsions d^6 V=d^3 X×d^3 P est indépendante de la position et de limpulsion (invariance de Poincaré).
Par conséquent , le nombre détat est proportionnel à lélément de volume
dN=(d^3 X×d^3 P)/(2;))^3 (;)=1)
Apres intégration sur les espaces des positions et des impulsions le nombre détat devient
;);)dN=1/;)(2;) );)^3 ;););)d^3 P;)
On définit la densité détat par unité dénergie ;)(E), comme un nombre détats ayant une énergie E et E+dE soit
;)(E)=dN/dE=1/;)(2;));)^3 P^2 dp/dE ;);)d;)
d;) est lélément de langle solide .
Mais lélément de volume d^3 P dans lespace des impulsions nest pas invariant de Lorentz alors que la quantité (d^3 P)/E lest . Un espace de phase
invariant de Lorentz quon peut lrécrire sous la forme :
;);)dN=;);)(d^3 P)/(2E;)(2pi);)^3 )
Comment je peux montrer que (d^3 P)/E est un invariant de Lorentz ?
Merci d'avance.
Invariance de lorentz
6 messages
- Page 1 sur 1
Bonsoir, si j'appelle P le quadrivecteur et p le vecteur associé, d^4P est explicitement invariant de Lorentz. Comme la relation de dispersion P² = m² est aussi explicitement invariante de Lorentz, sa réécriture en P0² = p² + m² = E(p)² l'est également. Donc \text{d}^4P) est invariant de Lorentz, et comme le choix d'une des deux branches solution P0 = +/- E(p) est invariant de Lorentz, on peut intégrer sans briser l'invariance en choisissant par exemple P0 = E(p), ce qui donne
est invariant de Lorentz, et comme le choix d'une des deux branches solution P0 = +/- E(p) est invariant de Lorentz, on peut intégrer sans briser l'invariance en choisissant par exemple P0 = E(p), ce qui donne }) .
.
Si tu n'aimes pas le 'détour intégral' proposé plus haut, tu peux simplement remarquer, que si tu fais un boost dans la direction de x avec une vitesse v (ça reste général, tu peux toujours te réorienter pour être dans ce cas), alors
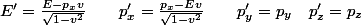
De plus, tu as = \sqrt{m^2+p^2} \quad \to \quad \frac{dE}{dp_x} =\frac{p_x}{E})
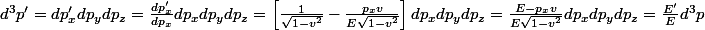
Tu en déduis donc que
 pour n'importe quel boost, donc cette mesure est invariante de Lorentz.
pour n'importe quel boost, donc cette mesure est invariante de Lorentz.
De plus, tu as
Tu en déduis donc que
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
