Relativité : question simple sur la transfo de Lorentz
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
calogerogigante
- Membre Naturel
- Messages: 16
- Enregistré le: 25 Juil 2010, 14:08
-
 par calogerogigante » 15 Sep 2010, 17:09
par calogerogigante » 15 Sep 2010, 17:09
Bonjour,
Je suis en train de lire un livre fantastique qui expose la théorie de la relativité, avec des maths de niveau moyen. Ce livre est consultable en ligne ici :
LIEBER - The Einstein theory of relativityAprès avoir introduit l'expérience de Michelson-Morley, l'auteur (Mme Lieber) détaille l'explication donnée par Lorentz, avec sa fameuse contraction.
Ma question est assez précise et concerne l'équation n°(5) à la page 17 du livre.
D'où ça sort ça :
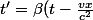)
Mme lieber ne semble pas dire d'où provient cet ajustement du temps t' du référentiel en mouvement. Y'a-t-il moyen de le savoir ?
-
Black Jack
 par Black Jack » 16 Sep 2010, 09:55
par Black Jack » 16 Sep 2010, 09:55
Je n'ai lu que 2 ou 3 lignes du lien et donc, il se peut que ce que vais écrire ne soit pas correct.
Le lien donne : x' = Beta.(x - vt)
Mais si on considère maintenant le "déplacement" de la lumière.
Comme la célérité de la lumière est indépendante du repère duquel on l'observe, on a alors : x' = c.t' et x = c.t (soit t = x/c)
x' = Beta.(x - vt)
ct' = Beta.(ct - v.x/c)
t' = Beta.(ct - v.x/c)/c
t' = Beta.(t - v.x/c²)
Avec les réserves d'usages.
:zen:
-
calogerogigante
- Membre Naturel
- Messages: 16
- Enregistré le: 25 Juil 2010, 14:08
-
 par calogerogigante » 16 Sep 2010, 10:18
par calogerogigante » 16 Sep 2010, 10:18
Waaaaouuuwww !
Merci BlackJack ! Je crois que c'est exactement ça !!!!
Tu es trop fort, si tu n'as lu que quelques lignes !!!!
Tout est clair maintenant et je peux continuer à avancer sans point noir dans la lecture de ce livre vraiment génial (consultable sur Google-Books) !
Merci merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
