Circuit CL
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 30 Déc 2006, 20:45
par Babe » 30 Déc 2006, 20:45
Bonjour à tous
voila j'ai quelque questions sur un circuit

ce circuit est facile mais je vois pas trop ce qu'il faut repondre pour chaque question
il me semble évident que:


merci d'avance
 par Dominique Lefebvre » 30 Déc 2006, 21:32
par Dominique Lefebvre » 30 Déc 2006, 21:32
bonsoir,
Tu peux repartir des définitions, ce sera plus clair!
Si un courant quasi-stationnaire i(t) circule dans une inductance et un condensateur:
- la tension aux bornes de l'inductance est v(t) = L*di(t)/dt
- le courant aux bornes du condensateur est i(t) = C*dv(t)/dt
Avec ça, tu peux calculer vs(t) en fonction de ve(t) et i(t), et le reste aussi..
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 30 Déc 2006, 21:57
par Babe » 30 Déc 2006, 21:57
par exemple pour la 1.1

j'ai Ve en fonction Vs mais comment je fais apparaitre i(t)
 par Dominique Lefebvre » 31 Déc 2006, 09:39
par Dominique Lefebvre » 31 Déc 2006, 09:39
Babe a écrit:par exemple pour la 1.1

j'ai Ve en fonction Vs mais comment je fais apparaitre i(t)
Fait attention aux conditions initiales dont tu auras besoin pour écrire l'équa diff! Qu'est-ce qui te permet de dire que la capa était chargée initialement (ton hypothèse q/C)?
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 31 Déc 2006, 15:43
par flaja » 31 Déc 2006, 15:43
bonjour,
pour faire disparaître "q", il faut utiliser la définition de i :
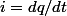
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 01 Jan 2007, 12:42
par Babe » 01 Jan 2007, 12:42
cela donne quoi pour la 1.1 parce que la je vois vraiment pas
Ve=Vs+..
merci d'avance
 par Dominique Lefebvre » 01 Jan 2007, 14:34
par Dominique Lefebvre » 01 Jan 2007, 14:34
Bonjour et meilleurs voeux...;
Tu es en présence d'un simple circuit auquel tu appliques la loi d'additivité des tensions...
Donc ve(t) = uc(t) + ul(t) , où uc(t)est la tension aux bornes du condensateur et ul(t) est la tension aux bornes de l'inductance et égale à vs(t).
Pour téablir ton équation différentielle, fait très attention à tes conditions initiales. A priori, ton énoncé ne dit rien sur la condition de charge du condensateur à t0 !
Tu devrais partir des définitions des tensions aux bornes de ces deux différents dipôles en fonction du temps.
 par Dominique Lefebvre » 01 Jan 2007, 14:35
par Dominique Lefebvre » 01 Jan 2007, 14:35
Babe a écrit:cela donne quoi pour la 1.1 parce que la je vois vraiment pas
Ve=Vs+..
merci d'avance
Autre précision aussi, n'écris pas Ve et Vs mais plutôt ve(t) et vs(t). Ce ne sont pas des constantes, mais des fonctions dépendantes du temps.
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 01 Jan 2007, 15:13
par Babe » 01 Jan 2007, 15:13
Dominique Lefebvre a écrit:Bonjour et meilleurs voeux...;
Donc Ve(t) = uc(t) + Vs(t) , où uc(t)est la tension aux bornes du condensateur et ul(t) est la tension aux bornes de l'inductance et égale à vs(t).
le problème c'est que je n'arrive pas a faire apparaitre le i(t) a la place du Uc(t)
 par Dominique Lefebvre » 01 Jan 2007, 16:01
par Dominique Lefebvre » 01 Jan 2007, 16:01
Babe a écrit:le problème c'est que je n'arrive pas a faire apparaitre le i(t) a la place du Uc(t)
Bonjour,
Flaja t'a donné la piste à suivre. Tu as uc(t) = q(t)/C et i(t) = dq(t)/dt
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 01 Jan 2007, 17:56
par Babe » 01 Jan 2007, 17:56
Dominique Lefebvre a écrit:Bonjour,
Flaja t'a donné la piste à suivre. Tu as uc(t) = q(t)/C et i(t) = dq(t)/dt
Uc(t)=Integrale(i(t))/C ?
 par Dominique Lefebvre » 01 Jan 2007, 18:57
par Dominique Lefebvre » 01 Jan 2007, 18:57
Babe a écrit:Uc(t)=Integrale(i(t))/C ?
Absolument! Mais fait gaffe aux conditions initiales (j'ai comme l'impression de me repéter:-))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités

