Vecteurs et colinéarité

[Dolfin34]

Bonjour !

J'ai une série d'exercices semblables mais je suis bloqué au premier !

Voici l’énoncé :

Soit ABCD un parallélogramme.

Soit E et F les points définis par :

Vecteur BE = 1 / 2 Vecteur AB et Vecteur AF = 3 Vecteur AD

Démontrer que les points C, E et F sont alignés.

J’ai trouvé que je dois utiliser cette propriété : Pour montrer que trois points C, E et F sont alignés, il faut prouver que les vecteurs CE et CF sont colinéaires.

Voila l’allure de la figure :



J’ai également trouvé cela :

Vecteur CF = Vecteur CA + Vecteur AF
Vecteur CF = Vecteur CD + Vecteur DF
Vecteur CF = Vecteur CB + Vecteur BF

Vecteur CE = Vecteur CA + Vecteur AE
Vecteur CE = Vecteur CD + Vecteur DE
Vecteur CE = Vecteur CB + Vecteur BE

Après je suis bloqué !
Je ne sais pas quelles égalités utiliser et je ne sais pas comment m’en servir !

J’espère que vous pourrez m’aider !

Merci d’avance !

[mathelot]

Bonsoir,

:id:

a) Les trois points A,B,D forment un repère du plan.

On peut donc calculer tous les vecteurs uniquement avec
et .


B) une fois les calculs faits, tu trouveras que
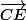
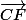
et sont colinéaires
(on passe de l'un à l'autre en multipliant par un nombre non nul)

[Dolfin34]

J'ai beau cherché, je ne trouve rien !
Vecteur AF = 3 Vecteur AD
Vecteur AE = 1.5 Vecteur AB

Suis-je sur la bonne piste ?

Merci encore !

[mathelot]

J'ai beau cherché, je ne trouve rien !
Vecteur AF = 3 Vecteur AD
Vecteur AE = 1.5 Vecteur AB

Suis-je sur la bonne piste ?

oui, tout à fait. :++:

On peut appliquer la règle du parallèlogramme:



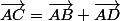
et un corollaire de la relation de Chasles:

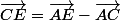
[Dolfin34]

Vecteur AC = Vecteur AB + Vecteur AD

Vecteur AD = Vecteur AC - Vecteur AB

Vecteur CF = CA + 3 AD
Vecteur CF = CA + 3 AC - 3 AD
Vecteur CF = 2 AC - 3AD
Vecteur CF = 2 AC + 3 DA
Vecteur CF = 1 DA + 2 DC

Vecteur AB = Vecteur AC - Vecteur AD

Vecteur CE = CA + 1.5 AB
Vecteur CE = CA + 1.5 AC - 1.5 AD
Vecteur CE = 0.5 AC - 1.5 AD
Vecteur CE = 0.5 AC + 1.5 DA
Vecteur CE = 1 DA + 0.5 DC

Est-ce juste ?

[mathelot]

Est-ce juste ?

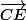
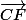
ben non, on doit trouver à la fin que et sont colinéaires

Là, les coordonnées que tu trouve ne forment pas un tableau de proportionnalité :hum:

Il y a une erreur de calcul :dodo:

[Dolfin34]

Mais alors, de quelle formule dois-je partir ?




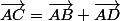
OU

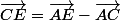
[Dolfin34]

Ou alors faut -il partir de

Vecteur AF = 3 Vecteur AD

Vecteur AE = 1.5 Vecteur AB

???

Merci d'avance car franchement, je ne comprends rien du tout !

[Dolfin34]

Je trouve maintenant :

AE = 1.5 AB
AB + AD = AC <=> CA = BA + DA
CE = CA + AE
CE = BA + DA + 1.5 AB
CE = DA + 0.5 AB

AF = 3 AD
AB + AD = AC <=> CA = BA + DA
CF = CA + AF
CF = BA + DA + 3 AD
CF = BA + 2 AD

Est-ce juste ?

[chaosleague2]

Oui il me semble,

CE = DA + 0.5 AB
CF = BA + 2 AD

Tu vois la proportionnalité?

[mathelot]

Oui il me semble,

CE = DA + 0.5 AB
CF = BA + 2 AD

Tu vois la proportionnalité?

Là, c'est ok. voiçi la fin:

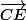
on multiplie par -2.



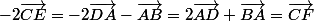
d'où

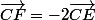
les deux vecteurs sont colinéaires et les trois points C,E,F alignés
(sur une même droite, comme aurait dit Mr de LaPallice :zen: ).

[Dolfin34]

OK ! Merci à vous deux !

J'en ai un autre :

Soit ABC un triangle.
On définit les points D et E tels que :
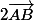
= + et =
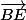
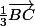
Montrer que les points A, D et E sont alignés.

= +
= +

= +
= + +
= +

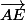
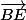
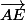
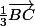
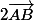
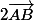
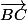
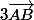
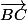
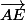
On multiplie par 3 :
= + =

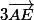
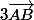
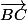
D'où = .

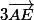
Donc, les vecteurs sont colinéaires et les points A, D, E sont alignés.

Est-ce juste ?

[chaosleague2]

Oui tout a fait :)

[Dolfin34]

Merci beaucoup !