Vecteur seconde
22 messages
- Page 1 sur 2 - 1, 2
Vecteur seconde
Bonjour,
(j'ai déjà poser mon problème mais personne ne m'a répondu sauf une personne et je n'ai pas compris, veuillez m'aidez svp)
J'éprouve quelques problèmes pour résoudre cet exercice de mathématiques:
ABC est un triangle. I est le milieu de [AC], K et L sont tels que :
(vecteur)AK= 3/5 (vecteur)AB et (vecteur)BL=2(vecteur)CB
Objectif: démontrer que les points I,K,L sont alignés.
a. calculez les coordonnées de I et de K.
* pour calculer les coordonnées de I : vu que I est le milieu de AC : xi=xa+xc/2 et yc: ya+yc/2
c'est ça ?
* pour K je n'ai pas d'idée.
b. en notant x et y les coordonnées de L, calculez les coordonnées de (vecteur)BL et (vecteur)2CB?
Déduisez-en celles de L?
je n'ai aucune idée.
2. Aide : Il reste à démontrer que les points I, K et L sont alignés. Il suffit pour cela de prouver, par exemple que (vecteur)IK et (vecteur)IL sont colinéaires.
- Calculez les coordonnées des vecteurs IK et IL
- Concluez
)J'ai vraiment des difficultées en math, je prend des cours particuliers mais mon prof n'est pas là. Ne croyez pas que je veux la réponse et basta, je veux comprendre et progresser).
Merci.
(j'ai déjà poser mon problème mais personne ne m'a répondu sauf une personne et je n'ai pas compris, veuillez m'aidez svp)
J'éprouve quelques problèmes pour résoudre cet exercice de mathématiques:
ABC est un triangle. I est le milieu de [AC], K et L sont tels que :
(vecteur)AK= 3/5 (vecteur)AB et (vecteur)BL=2(vecteur)CB
Objectif: démontrer que les points I,K,L sont alignés.
a. calculez les coordonnées de I et de K.
* pour calculer les coordonnées de I : vu que I est le milieu de AC : xi=xa+xc/2 et yc: ya+yc/2
c'est ça ?
* pour K je n'ai pas d'idée.
b. en notant x et y les coordonnées de L, calculez les coordonnées de (vecteur)BL et (vecteur)2CB?
Déduisez-en celles de L?
je n'ai aucune idée.
2. Aide : Il reste à démontrer que les points I, K et L sont alignés. Il suffit pour cela de prouver, par exemple que (vecteur)IK et (vecteur)IL sont colinéaires.
- Calculez les coordonnées des vecteurs IK et IL
- Concluez
)J'ai vraiment des difficultées en math, je prend des cours particuliers mais mon prof n'est pas là. Ne croyez pas que je veux la réponse et basta, je veux comprendre et progresser).
Merci.
math64 a écrit:Bonjour,
(j'ai déjà poser mon problème mais personne ne m'a répondu sauf une personne et je n'ai pas compris, veuillez m'aidez svp)
J'éprouve quelques problèmes pour résoudre cet exercice de mathématiques:
ABC est un triangle. I est le milieu de [AC], K et L sont tels que :
(vecteur)AK= 3/5 (vecteur)AB et (vecteur)BL=2(vecteur)CB
Objectif: démontrer que les points I,K,L sont alignés.
a. calculez les coordonnées de I et de K.
* pour calculer les coordonnées de I : vu que I est le milieu de AC : xi=xa+xc/2 et yc: ya+yc/2
c'est ça ?
* pour K je n'ai pas d'idée.
b. en notant x et y les coordonnées de L, calculez les coordonnées de (vecteur)BL et (vecteur)2CB?
Déduisez-en celles de L?
je n'ai aucune idée.
2. Aide : Il reste à démontrer que les points I, K et L sont alignés. Il suffit pour cela de prouver, par exemple que (vecteur)IK et (vecteur)IL sont colinéaires.
- Calculez les coordonnées des vecteurs IK et IL
- Concluez
)J'ai vraiment des difficultées en math, je prend des cours particuliers mais mon prof n'est pas là. Ne croyez pas que je veux la réponse et basta, je veux comprendre et progresser).
Merci.
Salut !
Il manque des données dans ton exos : si on veut des coordonnées il faut se donner un repère...
Je te propose de te placer dans le repère
a) Exprime donc les vecteurs
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Bonjour,
Tu ne devrais pas reposter un nouveau sujet mais continuer en re-questionnant dans l'ancien.
Ton énoncé est-il conforme à l'énoncé d'origine ? J'en doute un peu...
Tu évoques le calcul de coordonnées mais sans préciser dans quel repère :
) ? par exemple (ce qui serait plus "simple")...
? par exemple (ce qui serait plus "simple")...
Un repère orthonormé quelconque ?
Dans ce dernier cas, on pose :
, \;B(x_B;y_B),\;C(x_C;Y_C))
Et tu as bien ...
...
Les coordonnées du vecteur sont
sont )
Tu risques de ne pas beaucoup aimer la suite...
Les coordonnées de
donc;\frac 3 5(y_B-y_A)\right))
Est-ce que ce sont là pour autant les coordonnées de K ?
Si le l'origine du repère O est un point du plan différent de A, B ou c, alors la réponse est non...
Les coordonnées de K sont dans ce cas les coordonnées du vecteur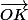
Et :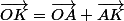
Avant de continuer (personnellement, j'arriverai au bout, mais c'est à toi que je pense), il me faudrait savoir si tu comprends ce que je fais et pourquoi je le fais
et surtout dans quel repère sont prises les coordonnées !!!!
Bye
Tu ne devrais pas reposter un nouveau sujet mais continuer en re-questionnant dans l'ancien.
Ton énoncé est-il conforme à l'énoncé d'origine ? J'en doute un peu...
Tu évoques le calcul de coordonnées mais sans préciser dans quel repère :
Un repère orthonormé quelconque ?
Dans ce dernier cas, on pose :
Et tu as bien
Les coordonnées du vecteur
Tu risques de ne pas beaucoup aimer la suite...
Les coordonnées de
donc
Est-ce que ce sont là pour autant les coordonnées de K ?
Si le l'origine du repère O est un point du plan différent de A, B ou c, alors la réponse est non...
Les coordonnées de K sont dans ce cas les coordonnées du vecteur
Et :
Avant de continuer (personnellement, j'arriverai au bout, mais c'est à toi que je pense), il me faudrait savoir si tu comprends ce que je fais et pourquoi je le fais
et surtout dans quel repère sont prises les coordonnées !!!!
Bye
Re,
Aaaahhhhh !
Je suis soulagé pour toi !
Dans ce repère les coordonnées de A, B, C sont
,\;B(1;0)) et
et )
D'où)
D'accord là-dessus ?
Dans ce repère les coordonnées de K sont donc les mêmes que celles du vecteur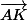 vois-tu pourquoi ?
vois-tu pourquoi ?
Donc le plan général est simple :
* calcul des coordonnées de
* tu en prends les 3/5
* tu as obtenu les coordonnées de K
Coordonnées de L
* calcul des coordonnées de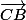
* tu en déduis les coordonnées de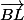
* tu calcules les coordonnées de (relation de Chasles)
(relation de Chasles)
* tu as donc les coordonnées de L
Colinéarité
* calcul des coordonnées de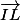 (par exemple)
(par exemple)
* calculs des coordonnées de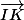
* comparaison des résultats pour trouver k réel tel que
* conclusion
Allez, au taf, reviens avec tes calculs (voire des questions)
Bye
math64 a écrit:c'est le repère (A; vecteur AB; vecteur AC)
Aaaahhhhh !
Je suis soulagé pour toi !
Dans ce repère les coordonnées de A, B, C sont
D'où
D'accord là-dessus ?
Dans ce repère les coordonnées de K sont donc les mêmes que celles du vecteur
Donc le plan général est simple :
* calcul des coordonnées de
* tu en prends les 3/5
* tu as obtenu les coordonnées de K
Coordonnées de L
* calcul des coordonnées de
* tu en déduis les coordonnées de
* tu calcules les coordonnées de
* tu as donc les coordonnées de L
Colinéarité
* calcul des coordonnées de
* calculs des coordonnées de
* comparaison des résultats pour trouver k réel tel que
* conclusion
Allez, au taf, reviens avec tes calculs (voire des questions)
Bye
Merci ! ;)
pour calculer les coordonnées de L vous me dites :
* calcul des coordonnées de \vec{CB}
* tu en déduis les coordonnées de \vec{BL}
* tu calcules les coordonnées de \vec{AL}=\vec{AB}+\vec{BL} (relation de Chasles)
ce que j'ai fais : CB (vecteur) = (1-0;0-1) = (1;-1)
2CB = (2;-2)
vecteur BL = (xl-1=2;yl-0=-2) = (3;-2)
je n'ai pas utiliser la relation de Chasles ....
Ma méthode est-elle bonne ? et la réponse ?
Merci.
pour calculer les coordonnées de L vous me dites :
* calcul des coordonnées de \vec{CB}
* tu en déduis les coordonnées de \vec{BL}
* tu calcules les coordonnées de \vec{AL}=\vec{AB}+\vec{BL} (relation de Chasles)
ce que j'ai fais : CB (vecteur) = (1-0;0-1) = (1;-1)
2CB = (2;-2)
vecteur BL = (xl-1=2;yl-0=-2) = (3;-2)
je n'ai pas utiliser la relation de Chasles ....
Ma méthode est-elle bonne ? et la réponse ?
Merci.
Re,
Bah, on est toujours "lourd" par rapport à quelqu'un. C'est bien de chercher à comprendre : c(est la seule façon d'avancer...
Tu as besoin des coordonnées du point L...
Dans le repère) les coordonnées de L sont celles du vecteur
les coordonnées de L sont celles du vecteur 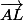 , A étant l'origine des coordonnées
, A étant l'origine des coordonnées
Et comme ces coordonnées tu ne les connais pas il faut bien que tu les calcules...
Comment ?
C'est là qu'intervient la relation de Chasles parce que les coordonnées de ces deux vecteurs te sont connues (relis la discussion).
parce que les coordonnées de ces deux vecteurs te sont connues (relis la discussion).
Ayé ?
Sinon, qu'est-ce qui t'arrête ?
Bye
Bah, on est toujours "lourd" par rapport à quelqu'un. C'est bien de chercher à comprendre : c(est la seule façon d'avancer...
math64 a écrit:ah mais oui je suis bête ! mais d'où vous sortez AL ?
[B]
Tu as besoin des coordonnées du point L...
Dans le repère
Et comme ces coordonnées tu ne les connais pas il faut bien que tu les calcules...
Comment ?
C'est là qu'intervient la relation de Chasles
Ayé ?
Sinon, qu'est-ce qui t'arrête ?
Bye
Youupii sa me fait plaisir :D
2. Il reste à démontrer que les points I, K et L sont alignés. Il suffit pour cela de prouver, par exemple que (vecteur)IK et (vecteur)IL sont colinéaires.
- Calculez les coordonnées des vecteurs IK et IL
- Concluez
j'ai calculer IK (xk-xi;yk-yi) soit IK (3/5-0;0-1/2) alors IK 3/5-1/2= -3/10
j'ai calculer IL (xl-xi;yl-yi) soit IL (3-0;-2-1/2) alors IK 3/-5/2 = -6/5
j'essaye de trouver le réel k :
IK=k*IL
-3/10=k*-6/5
k= -3/10+-6/5
k= -3/2
sa colle pas pck quand je fais k*IL = -3/2*-6/5 je trouve 9/5 et pas IK soit -3/10
Merci de bien vouloir m'aider
2. Il reste à démontrer que les points I, K et L sont alignés. Il suffit pour cela de prouver, par exemple que (vecteur)IK et (vecteur)IL sont colinéaires.
- Calculez les coordonnées des vecteurs IK et IL
- Concluez
j'ai calculer IK (xk-xi;yk-yi) soit IK (3/5-0;0-1/2) alors IK 3/5-1/2= -3/10
j'ai calculer IL (xl-xi;yl-yi) soit IL (3-0;-2-1/2) alors IK 3/-5/2 = -6/5
j'essaye de trouver le réel k :
IK=k*IL
-3/10=k*-6/5
k= -3/10+-6/5
k= -3/2
sa colle pas pck quand je fais k*IL = -3/2*-6/5 je trouve 9/5 et pas IK soit -3/10
Merci de bien vouloir m'aider
Ren
Mais 'kestufé" ??????
C'est quoi ces calculs ? Pourquoi additionner abscisses et ordonnées ? Les cordonnées restent au nombre de deux !
Pour moi :
 et
et 
D'où)
Et pour toi ?
Allez, ressaisis-toi, va manger ou boire quelque chose, prends une douche froide (enfin... ptêt pas... la t° ne s'y prête pas !)...
Et reviens et continue, t'es au bout... !!!
Bye
math64 a écrit:Youupii sa me fait plaisir
j'ai calculer IK (xk-xi;yk-yi) soit IK (3/5-0;0-1/2) alors IK 3/5-1/2= -3/10
j'ai calculer IL (xl-xi;yl-yi) soit IL (3-0;-2-1/2) alors IK 3/-5/2 = -6/5
Mais 'kestufé" ??????
C'est quoi ces calculs ? Pourquoi additionner abscisses et ordonnées ? Les cordonnées restent au nombre de deux !
Pour moi :
D'où
Et pour toi ?
Allez, ressaisis-toi, va manger ou boire quelque chose, prends une douche froide (enfin... ptêt pas... la t° ne s'y prête pas !)...
Et reviens et continue, t'es au bout... !!!
Bye
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
