Vecteur colinéaire

[so213]

Bonjour, j'ai un Dm à faire et une question me pose problème :

1/ On considère les point A(2;-t) , B(t+2;1), C (1;2) et D (t;t)
Déterminer t pour que (AB) et (CD) soient parallèles.
Ma réponse:
Vecteur AB : (t;t+1)
Vecteur CD: ((1-t);(2-t))
On applique relation de colinéarité:
xy' - x'y=0
(t*(2-t)) - ((1-t)*(t+1)) = 0
2t-t^2-t-1+t^2+t=0
2t=1
t=1/2
C'est juste ?

2/ On considère les points E(2;2), F(t;4) et G(10;t)
Déterminer t pour que E, F et G soient alignés.
Vecteur EF : (t;t+1)
Vecteur EG: ((1-t);(2-t))
On applique relation de colinéarité:
xy' - x'y=0
((2-t)*(2-t)) - (8*2)
4-2t-2t+t^2-16=0
-4t + t^2 =0
t*(-4+t)=0
donc t=0
-4 + t =0
t=4
C'est juste ???
On considère les points H(-2;0), I (2t ; t+1) et J(4t ; 2t+1).
Démontrer que, quelle que soit la valeur de t, H, I et J sont alignés.
Je n'arrive pas :hum: :hum:
Merci beaucoup

[laetidom]

Bonjour, j'ai un Dm à faire et une question me pose problème :

1/ On considère les point A(2;-t) , B(t+2;1), C (1;2) et D (t;t)
Déterminer t pour que (AB) et (CD) soient parallèles.
Ma réponse:
Vecteur AB : (t;t+1) OK
Vecteur CD: ((1-t);(2-t)) ------------------> t-1 ; t-2
On applique relation de colinéarité:
xy' - x'y=0
(t*(2-t)) - ((1-t)*(t+1)) = 0
2t-t^2-t-1+t^2+t=0
2t=1
t=1/2 -----------> ça revient au même t=0.5 et comme 0.5.-1.5 - (-0.5.1.5) = 0 donc vectAB // vectCD donc t=0.5 est juste
C'est juste ?

2/ On considère les points E(2;2), F(t;4) et G(10;t)
Déterminer t pour que E, F et G soient alignés.
Vecteur EF : (t;t+1) ----???------------> (t-2 ; 2)
Vecteur EG: ((1-t);(2-t)) ---???------------> (8 ; t-2)
On applique relation de colinéarité:
xy' - x'y=0
((2-t)*(2-t)) - (8*2)
4-2t-2t+t^2-16=0
-4t + t^2 =0
t*(-4+t)=0
donc t=0
-4 + t =0
t=4 si t=4 alors 4.(-2) - [5.3] "est = à 0 ?" = -23 différent de 0
C'est juste ??? =====> essaye avec mes coordonnées des vecteurs EF et EG....2 valeurs de t possibles....
On considère les points H(-2;0), I (2t ; t+1) et J(4t ; 2t+1).
Démontrer que, quelle que soit la valeur de t, H, I et J sont alignés.
Je n'arrive pas :hum: :hum:
Merci beaucoup

Attention......................

[so213]

D'accord et comment on fait pour la 3 ???

[laetidom]

D'accord et comment on fait pour la 3 ???

....je regardes....

déjà, H est un point fixe et les coordonnées de I et J sont proportionnelles........... :

............on passe de xI à xJ ------------> de 2t à 4t

............on passe de yI à yJ ------------> de 1t+1 à 2t+1

[laetidom]

Pour prouver le 3)

tu calcules en fonction de t la pente de HI puis celle de HJ, si elles sont les mêmes c'est que le résultat est le même et si de plus le résultat du calcul n'est pas fonction de t on aurait répondu à la question....

[laetidom]

pente de HI =" " = = ... =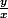

pente de HJ = = ... =

.....les résultats sont égaux donc alignement de H, I et J avec une pente de 0.5 (ou , c'est-à-dire que si tu fais 1 à l'horizontale, tu fais 0.5 à la verticale) qui n'est pas fonction de t, donc quelque soit t ces 3 points sont alignés.....

A tu-compris ?....