Valeur d'un complexe

[ghalyb24]

Bonjour
J'ai un probleme avec une question, je voudrai trouver la valuer du complexe:

(-1+(i*racine(3))^2010) + (-1-(i*racine(3))^2010)
On voit bien que cela correspond à :
z^2010 + zBARRE^2010 .
Mais que faire après?
Merci.

[fatal_error]

salut,

ca correspond avec ET 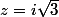(que tu peux simplifier en disant ET )
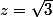en passant en exponentielle ()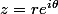
on a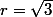 et
on a
le membre parenthèsé devrait t'évoquer quelques souvenirs

[Tiruxa47]

Bonjour,
Attention !
z est -1+i racine(3) soit 2j avec j racine cubique de l'unité donc j^3=1

Comme 2010 = 3*670

j^2010 = 1

ne pas oublier le 2^2010 toutefois

idem pour le second terme avec j barre

[zygomatique]

salut





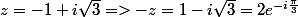
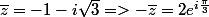
par conséquent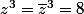

or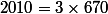

donc ...

EDIT :: msg corrigé suite à la remarque de Tiruxa ... que je remercie encore

[fatal_error]

le parenthèsage me semble pourtant clair:
(-1+(i*racine(3))^2010) ... = -1+(i*racine(3))^2010 ... = -1 + z^2010
avec z = i racine(3)

[Tiruxa47]

Ok fatal_error mais ghalyb24 nous dit z^2010 je pense qu'il a fait une erreur de parenthésage mais c'est une opinion perso.

Ceci dit zygomatique |1-i racine(3)| = 2 non pas 1/2

[zygomatique]

damned ... je corrige ...

merci ...

[Black Jack]

ghalyb54 a écrit un équivalent à ceci :



Mais par son "cela correspond à : z^2010 + zBARRE^2010", on peut se demander si son intention n'était pas d'écrire :



Va savoir, alors ce qu'a vraiment voulu écrire ghalyb54...