Une équation réciproque

[busard_des_roseaux]

[Carpate]

Ah oui excusez moi... Est-ce que je supprime cette conversation?

Non, mais indique où tu en es et ce qui te bloque sur le premier fil

[Proriko]

En réalité j'avoue être complétement perdu...
J'ai pas vraiment compris pourquoi il faut diviser

[busard_des_roseaux]

J'ai pas vraiment compris pourquoi il faut diviser

quand on divise par apparaissent les quantités

x

et


qui ressemble beaucoup au carré de la précédente.

ça laisse espérer se ramener à une équation de degré 2 par changement de variable.

[Proriko]

Je suis perdu de ce que nous avons fait hier , merci en tout cas pour la division

b.Démontrer que x est une solution si et seulement si 1/x est solution

[Proriko]

Diviser par x^4 permet de démontrer que x et 1/x sont solutions donc ?

Cela répond donc à la question : démontre que x est solution si et seulement si 1/x est solution

[busard_des_roseaux]

Je suis perdu de ce que nous avons fait hier , merci en tout cas pour la division

b.Démontrer que x est une solution si et seulement si 1/x est solution

on doit tout reprendre ? :hum:

[busard_des_roseaux]

Diviser par x^4 permet de démontrer que x et 1/x sont solutions donc ?

Cela répond donc à la question : démontre que x est solution si et seulement si 1/x est solution

oui...........................

[Proriko]

Oui je pense ... mais je vais essayé de dire ce dont je me souviens :
Pour démontrer que x et 1/x sont solutions on utilise 1/x^4? ou du moins on divise l'équation (E) par x^4 ?

[busard_des_roseaux]

oui.....................

[Proriko]

Mais pourquoi diviser par x^4 et non par x^3 ou x² ou juste x ?

[Carpate]

Je suis vraiment désolé ca ne se reproduira plus.
En réalité j'avoue être complétement perdu...
J'ai pas vraiment compris pourquoi il faut diviser

Disons que la méthode fonctionne et permet de faire apparaître une nouvelle inconnue

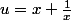
On regroupe les termes de même coefficient :
(1)
Changement d'inconnue
Il faut exprimer en fonction de u


L'équation (1) devient :
ou
Résous cette équation --> et
Les 4 racines en x, seront données par les 2 équations du second degré :



Remarque :
Tu pourras ne calculer qu'une racine de chaque équation et exploiter ce qu'on t'a demandé de démontrer au tout début : Si x est solution, alors 1/x est solution

[Proriko]

Je ne comprend toujours pas pourquoi on ne diviserais pas par x² x^3 ou juste x ?

[Proriko]

Comment passe t-on de x²+2x1/x+1/x² à x²+1/x²+2 ?

[Carpate]

Comment passe t-on de x²+2x1/x+1/x² à x²+1/x²+2 ?

Mets des parenthèses c'est illisible !

[Proriko]

Lorsque que l'on veut exprimer x²+1/x² en fonction de U pouvez vous m'expliquez la premier ligne que vous avez écrit?

[busard_des_roseaux]

calcule avec la somme remarquable

[Proriko]

J'ai bien compris mais 1/x² = 2 ?

[Carpate]

Lorsque que l'on veut exprimer x²+1/x² en fonction de U pouvez vous m'expliquez la premier ligne que vous avez écrit?

Je trouve que tu exagères un peu :
- tu mobilises au moins 3 personnes sur 2 fils différents
- lorsque on te fournit un calcul détaillé comme celui-ci :
, au lieu de le refaire calmement en prenant une feuille de papier et un crayon tu demandes aussitôt une explication supplémentaire.
C'est quand même étonnant que tu ne saches pas utiliser une identité remarquable !

[Proriko]

Ce n'est pas vraiment ma tasse de thé je dois l'avouer.
Je sais faire une identité remarquable mais sous cette forme je trouve ça assez compliquer