Type bac

[jenli]

bonsoir
j'ai un probleme pour cet exercice. j'ai besoin d'aide si possible
voici l'enonce
f est la fonction definie sur R par : f(x) = x + racine carre x² +1
C la courbe representatrice de f dans un repere ( O;i;j)
1) etudiez la limite de f en - l'infini . interpretez graphiquement ce resultat
2) prouvez que la droite d'équation y = 2x est asymptote oblique à C en + l'infini
3) etudiez la position relative de C et de Delta
merci d'avance

[Mortelune]

Bonsoir, pour la première question essaye de factoriser f par x :)

[Rebelle_]

B'jour =)

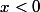
NB : si alors , ici on étudie bien la limite en - l'infini. C'est important à savoir lorsque l'on veut "sortir" le carré de la racine carrée

[Mortelune]

Ah oui aussi je ne sais plus quels outils vous avez ou pas donc pour t'aider tu peux utiliser un taux d'accroissement de la fonction racine carrée.

[jenli]

c'est quoi un taux d'accroissement

[Mortelune]

Normalement tu as vu ça en première avec les cours sur la dérivation, peut être ne l'as tu pas appelé comme ça :

http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/node3.html

[jenli]

je n'ai jamais vu le taux d'accroisement meme en première

[Mortelune]

C'est bizarre, c'est quand même ce qui défini la dérivée en un point d'une fonction ><

[jenli]

moi j'ai vu f' la dérivée mais pas le taux d'accroisement

[Mortelune]

Alors je te conseille de regarder la seconde définition du lien que j'ai mis plus haut, ça pourrait t'aider ;)

[jenli]

je trouve pour la limite car je n'ai jamai apri a calculé une limite avec une dérivée donc je trouve une limite qui est indeterminé car linfini +- linfini donc je suis coincé pouvait vous m'aider?

[Mortelune]

On a
On factorise par x donc (voir la remarque de Rebelle)

Regardons
Donc
On sait de plus que

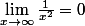
On va donc écrire g(x) pour faire apparaître un taux d'accroissement.

Or on observe le taux d'accroissement de la fonction racine carrée en 1 :

D'où

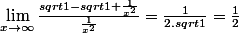
On en déduit que :

[jenli]

je ne comprends pas votre raisonnement

[Mortelune]

Tu ne comprends pas l'utilisation du taux d'accroissement ou c'est avant ?

[jenli]

avant et aussi le taux d'accroissement

[Mortelune]

Pour le taux d'accroissement je te renvoie sur la définition je peux pas faire grand chose de plus si tu n'as pas d'outils pour lever ton indétermination :/

Avant qu'est-ce que tu ne vois pas que je ne ré-explique pas tout si ce n'est pas la peine.

[jenli]

le tout
du raisonnement

[Mortelune]

C'est la question 1) de ton exercice, on va chercher à transformer l'écriture de la fonction f pour pouvoir lever l'indétermination sur sa limite en et utiliser certaines propriété sur le calcul des limites.
Sans plus de précision je ne vois pas trop comment en dire "plus".

[jenli]

commet obtient on f(x)= x²

[Mortelune]

On n'obtient pas f(x)=x², fin si c'est le cas c'est pas volontaire.