Trouver l'affixe du sommet d'un triangle équilatéral dans un
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Inscription
- Membre Naturel
- Messages: 76
- Enregistré le: 25 Oct 2013, 13:12
-
 par Inscription » 24 Jan 2015, 13:09
par Inscription » 24 Jan 2015, 13:09
Bonjour,
Dans un plan complexe, j'ai un triangle ADE qui est équilatéral direct. Le point A a pour affixe i, le point D a pour affixe 1 et je dois démontrer que le point E a pour affixe
(1+i))
.
J'ai donc utilisé le théorème qui dit que le triangle ADE est équilatéral direct si et seulement si
} \,+ \,zE * (\exp{(\frac{i2\pi}{3}))}^2)
mais après avoir remplacé les affixes que je connais, j'obtiens

et je ne sais plus quoi faire. Pourriez-vous m'aider ? Merci d'avance.
-
mathelot
 par mathelot » 24 Jan 2015, 13:31
par mathelot » 24 Jan 2015, 13:31
bjr,
équation d'inconnue E:
=\vec{DA})
r: rotation traduite par
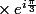
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 24 Jan 2015, 13:37
par Manny06 » 24 Jan 2015, 13:37
Inscription a écrit:Bonjour,
Dans un plan complexe, j'ai un triangle ADE qui est équilatéral direct. Le point A a pour affixe i, le point D a pour affixe 1 et je dois démontrer que le point E a pour affixe
(1+i))
.
J'ai donc utilisé le théorème qui dit que le triangle ADE est équilatéral direct si et seulement si
} \,+ \,zE * (\exp{(\frac{i2\pi}{3}))}^2)
mais après avoir remplacé les affixes que je connais, j'obtiens

et je ne sais plus quoi faire. Pourriez-vous m'aider ? Merci d'avance.
tu sais déjà que AE=ED
donc E(x,x)
ensuite (DE,DA)=pi/3
donc ZA-ZD=e^(ipi/3)(ZE-ZD)
i-x(1+i)=(1/2+iV3/2)[x(1+i)-1)
-
Inscription
- Membre Naturel
- Messages: 76
- Enregistré le: 25 Oct 2013, 13:12
-
 par Inscription » 24 Jan 2015, 14:12
par Inscription » 24 Jan 2015, 14:12
mathelot a écrit:bjr,
équation d'inconnue E:
=\vec{DA})
r: rotation traduite par
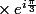
Je n'ai jamais étudié ce dont vous me parlez
-
Inscription
- Membre Naturel
- Messages: 76
- Enregistré le: 25 Oct 2013, 13:12
-
 par Inscription » 24 Jan 2015, 14:13
par Inscription » 24 Jan 2015, 14:13
Manny06 a écrit:tu sais déjà que AE=ED
donc E(x,x)
ensuite (DE,DA)=pi/3
donc ZA-ZD=e^(ipi/3)(ZE-ZD)
i-x(1+i)=(1/2+iV3/2)[x(1+i)-1)
Je ne comprends pas comment vous obtenez zA-zD.
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 24 Jan 2015, 15:01
par Manny06 » 24 Jan 2015, 15:01
Inscription a écrit:Bonjour,
Dans un plan complexe, j'ai un triangle ADE qui est équilatéral direct. Le point A a pour affixe i, le point D a pour affixe 1 et je dois démontrer que le point E a pour affixe
(1+i))
.
J'ai donc utilisé le théorème qui dit que le triangle ADE est équilatéral direct si et seulement si
} \,+ \,zE * (\exp{(\frac{i2\pi}{3}))}^2)
mais après avoir remplacé les affixes que je connais, j'obtiens

et je ne sais plus quoi faire. Pourriez-vous m'aider ? Merci d'avance.
Peux tu préciser le théorème que tu cites car je ne vois pas d'égalité
si c'est égal 0
il suffit que tu multiplies ta fraction haut et bas par e^(-i4pi/3)
ensuite développes en remplaçant partout e^it par cost +isint
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 24 Jan 2015, 16:27
par Manny06 » 24 Jan 2015, 16:27
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 380 invités
