Un triangle

[Dacu]

Bonjour à tous,

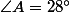
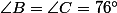
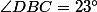
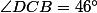
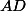
Dans le triangle avec et , nous prenons le point .Si et , alors comment divise-t-il la moitié droite l'angle ?

Cordialement,

Dacu

[pascal16]

J'ai pas bien compris l'énoncé
si tu appelle x l'angle cherché, je pense qu'en écrivant le fait que dans tous les triangles à l'intérieur de ABC la somme des angles vaut 180, ça va te donner une équation en x.

[chan79]

c'est peut-être ça:

[DabbieQing3]

Salut! Je suis content de vous voir.
J'ai deux solutions.
http://www.casimages.com/i/180113052108858833.jpg.html

[DabbieQing3]

C'est le second procédé. merci!
http://www.casimages.com/i/180113053015270303.jpg.html
http://www.casimages.com/i/18011305314446709.jpg.html
je vous demande pardon. Je ne sais pas comment télécharger des photos.
Je vous remercie de votre image!

[chan79]

salut
Avec la forme trigonométrique du théorème de Ceva, on arrive à


et si on transforme tan(21)=sin(14+7)/cos(14+7) on arrive à la même chose.
Calculs pénibles mais qui aboutissent.
Il y a peut-être une solution géométrique (angles inscrits, bissectrices ... ?)

[DabbieQing3]

salut
Avec la forme trigonométrique du théorème de Ceva, on arrive à


et si on transforme tan(21)=sin(14+7)/cos(14+7) on arrive à la même chose.
Calculs pénibles mais qui aboutissent.
Il y a peut-être une solution géométrique (angles inscrits, bissectrices ... ?)

(sin 14)(1+2cos14)=sin14+sin28=2sin(21)cos(7)
et: (cos14+1)(2cos14-1)=2(cos14)^2-1+cos14=cos28+cos14=2cos(21)cos(7)
Alors， tan(BAD)=tan21 so we got : BAD=21
Votre solution est correcte！

[Dacu]

Salut! Je suis content de vous voir.
J'ai deux solutions.
http://www.casimages.com/i/180113052108858833.jpg.html

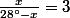
Très bien!La relation et je l'ai trouvé , mais je ne savais pas quoi faire ensuite ... Et les autres solutions sont belles...Enfin, il s'ensuit que .Merci très beaucoup!

Cordialement,

Dacu

[chan79]

Oui, mais il me semble qu'il y a une solution géométrique plus élégante. J'ai dû déjà voir passer cet exo ...