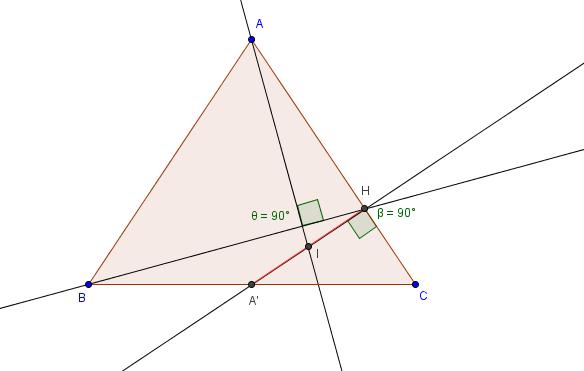
Bonsoir, j'ai trouvé une solution (pas très élégante car très calculatoire mais qui marche) qui consiste à introduire une repère orthonormé. J'ai pris
avec le vecteur
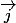
de même norme que
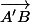
et orthogonal à (BC) pour bien avoir un repère orthonormé.
Ensuite comme le triangle est isocèle en A, on peut en déduire que les coordonnées de A sont de la forme (0,a) avec
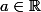
. De même on a : B=(-1,0), C=(1,0). Ensuite il faut trouver les coordonnées de H, il y a plusieurs possibilités pour cela, j'ai trouvé :
)
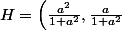. On en deduit ensuite facilement les coordonnées de I (c'est simplement la moitié pour chaque composante).
A partir des coordonnées de tous ces points, on peut calculer les coordonnées des vecteurs
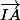
et
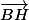
. Puis comme le repère est orthonormé on sait que le produit scalaire usuel de deux vecteur s'annule quand ces vecteur sont orthogonaux. Donc on fait simplement le produit scalaire de ces deux vecteurs et voit que celui-ci est nul ce qui implique que les vecteurs
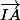
et
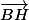
sont orthogonaux et il en est donc de même pour les droites (BH) et (IA).
Bon, le fait de ramener un problème de géométrie à un problème d'algèbre en introduisant un repère est en général efficace mais ce n'est pas toujours la solution la plus rapide donc si quelqu'un trouve la solution avec les triangles semblables je suis preneur...
![[IMG]http://img7.imageshack.us/img7/8610/triangler.jpg[/img]](http://img7.imageshack.us/my.php?image=triangler.jpg){kind=link}