Le théorème d'Aubry est-il au programme de TS spé maths ?

[M.Floquet]

Bonjour il s'agit de celui-ci :
Si le cercle (C) : x²+y²=n passe par un point à coordonnées rationnelles alors il passe aussi par un point à coordonnées entières.

Merci d'avance

[capitaine nuggets]

Salut !

Bonjour il s'agit de celui-ci :
Si le cercle (C) : x²+y²=n passe par un point à coordonnées rationnelles alors il passe aussi par un point à coordonnées entières.

Merci d'avance

Pas à ma connaissance et en plus la plupart des élèves ne savent pas toujours bien pas ce qu'est un nombre rationnel.

[M.Floquet]

Salut !



Pas à ma connaissance et en plus la plupart des élèves ne savent pas toujours bien pas ce qu'est un nombre rationnel.

Merci bien, mais je pense qu'il pourrait quand même tomber aux Olympiades

[Lostounet]

Très intéressant ! Mais malheureusement il n'est pas au programme de TS normalement...
La preuve m'intéresse si elle est accessible à mon niveau.

[M.Floquet]

Très intéressant ! Mais malheureusement il n'est pas au programme de TS normalement...
La preuve m'intéresse si elle est accessible à mon niveau.

Je trouve que sur cette page http://www.mathforu.com/pdf/theoreme-aubry.pdf elle est très bien expliquée et accessible largement en terminale (quelques notions d'arithmétiques sont nécessaires) car de mémoire, savoir paramétrer une droite c'est censé être acquis en terminale.
Une généralisation de ce théorème est : le théorème des quatre carrés de Lagrange mais celui-là est plus technique il me semble.

[Lostounet]

Merci je vais regarder ça !

[paquito]

Merci beaucoup pour cet apport culturel,

Par contre, la démonstration présente beaucoup trop de difficultés; si les élèves savent trouver une représentation paramétrique dans l'espace, ce n'est pas une représentation paramétrique dans le plan qui peut poser problème (à ce propos c'est pour t=-1 que M=P, ce qui ne change pas grand chose à la démonstration); mais on travaille avec 7 paramètres, ce qui bien sûr ne peut pas passer; déjà, "il est clair que P' existe" ne sera pas une évidence; il faudra faire un quadrillage du plan, considérer que P est dans un carré (évident) et montrer que la distance de P à un des sommet ne peut excéder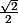 , ce qui est là tout à fait faisable; par contre, trouver les coordonnées du point Q à partir de la solution évidente t=-1 nécessite déjà d'avoir trouvé l'équation du second degré avec 1 inconnue et 7 paramètres, ce qui n'est pas du tout dans l'"esprit" du programme où si un calcul est trop difficile, on utilise un logiciel de calcul formel! Quant à la fin de la démonstration, elle est hors de portée de nos élèves.
Regarder ce que l'on demande au bac et vous comprendrez.
Ceci dit, c'est très gentil de votre part de nous proposer un problème très intéressant.

[M.Floquet]

Merci beaucoup pour cet apport culturel,

Par contre, la démonstration présente beaucoup trop de difficultés; si les élèves savent trouver une représentation paramétrique dans l'espace, ce n'est pas une représentation paramétrique dans le plan qui peut poser problème (à ce propos c'est pour t=-1 que M=P, ce qui ne change pas grand chose à la démonstration); mais on travaille avec 7 paramètres, ce qui bien sûr ne peut pas passer; déjà, "il est clair que P' existe" ne sera pas une évidence; il faudra faire un quadrillage du plan, considérer que P est dans un carré (évident) et montrer que la distance de P à un des sommet ne peut excéder , ce qui est là tout à fait faisable; par contre, trouver les coordonnées du point Q à partir de la solution évidente t=-1 nécessite déjà d'avoir trouvé l'équation du second degré avec 1 inconnue et 7 paramètres, ce qui n'est pas du tout dans l'"esprit" du programme où si un calcul est trop difficile, on utilise un logiciel de calcul formel! Quant à la fin de la démonstration, elle est hors de portée de nos élèves.
Regarder ce que l'on demande au bac et vous comprendrez.
Ceci dit, c'est très gentil de votre part de nous proposer un problème très intéressant.

Arf ça remonte à loin la TS mais bon cet exercice mêlant arithmétique et géométrie me semble être pas mal pour ceux qui souhaitent s'engager prochainement dans une fac de maths ou MPSI. Je dois admettre que pour l'existence du point P' une indication (ou une explication plus touffue) serait la bienvenue.

[paquito]

Arf ça remonte à loin la TS mais bon cet exercice mêlant arithmétique et géométrie me semble être pas mal pour ceux qui souhaitent s'engager prochainement dans une fac de maths ou MPSI. Je dois admettre que pour l'existence du point P' une indication (ou une explication plus touffue) serait la bienvenue.

Je suis tout à fait d'accord en ce qui concerne l'intérêt de cet exercice, mais il ne peut être abordable que pour une toute petite minorité d'élèves. On trouve maintenant en TS des élèves qui écrivent
(x-1)²=x²-1! Donc on se limite à préparer les classiques du bac, ce qui limite beaucoup de choses....

[Ben314]

Je trouve que sur cette page http://www.mathforu.com/pdf/theoreme-aubry.pdf

Je sais pas si, comme le dit paquito, elle "présente beaucoup trop de difficultés", mais par contre, ce que je vois, c'est que telle qu'elle elle me semble "bien fausse" et ça sent la recopie d'une preuve correcte par quelqu'un qui n'a pas compris la preuve.

Si on suis la preuve, on part d'une solution et on en fabrique une nouvelle de la forme où 0<e<bd.
L'auteur affire ensuite que, "si on recommence le procédé on obtient une solution où 0<f<e..."
Étonnant : perso, j'aurais bien pensé que, lorsque b=d=e, le produit bd il valait e^2 et pas e...

Bon, en fait le principe marche (c'est pour ça que je soupçonne l'auteur d'avoir pompé ailleurs) , mais a mon avis, la rédaction ne va pas : ce qu'il faut obtenir comme conclusion du calcul, c'est 0<e<ppcm(b,d) et tout est nettement plus clair si, au départ, les deux rationnels a/b et c/d on suppose qu'on les as réduit au même dénominateur et qu'ils s'écrivent a/c et b/c : on obtient alors directement 0<e<c et ça roule.

P.S. Je suis d'acord que, si on suis et qu'on comprend parfaitement bien les calculs, on voit que, dans le cas où b=d, on peut améliorer la majoration par 0<e<b à la place de 0<e<bd, mais ça serait bien de le signaler plutôt que de faire comme si on reprenait la deuxième fois exactement les même méthode que la première fois...

P.S.2. : Bien qu'historiquement parlant, ce type de preuve soit attribué à Fermat avec ces fameuses "descentes infinies", je me demande toujours si, pédagogiquement parlant, c'est pas plus simple en considérant au départ une solution minimale (ici de dénominateur minimal) ce qui permet d'avoir une seule "étape" pour conclure.

[M.Floquet]

Je sais pas si, comme le dit paquito, elle "présente beaucoup trop de difficultés", mais par contre, ce que je vois, c'est que telle qu'elle elle me semble "bien fausse" et ça sent la recopie d'une preuve correcte par quelqu'un qui n'a pas compris la preuve.

Si on suis la preuve, on part d'une solution et on en fabrique une nouvelle de la forme où 0<e<bd.
L'auteur affire ensuite que, "si on recommence le procédé on obtient une solution où 0<f<e..."
Étonnant : perso, j'aurais bien pensé que, lorsque b=d=e, le produit bd il valait e^2 et pas e...

Bon, en fait le principe marche (c'est pour ça que je soupçonne l'auteur d'avoir pompé ailleurs) , mais a mon avis, la rédaction ne va pas : ce qu'il faut obtenir comme conclusion du calcul, c'est 0<e<ppcm(b,d) et tout est nettement plus clair si, au départ, les deux rationnels a/b et c/d on suppose qu'on les as réduit au même dénominateur et qu'ils s'écrivent a/c et b/c : on obtient alors directement 0<e<c et ça roule.

P.S. Je suis d'acord que, si on suis et qu'on comprend parfaitement bien les calculs, on voit que, dans le cas où b=d, on peut améliorer la majoration par 0<e<b à la place de 0<e<bd, mais ça serait bien de le signaler plutôt que de faire comme si on reprenait la deuxième fois exactement les même méthode que la première fois...

P.S.2. : Bien qu'historiquement parlant, ce type de preuve soit attribué à Fermat avec ces fameuses "descentes infinies", je me demande toujours si, pédagogiquement parlant, c'est pas plus simple en considérant au départ une solution minimale (ici de dénominateur minimal) ce qui permet d'avoir une seule "étape" pour conclure.

Un fan d'arithmétique Ben ?

[Ben314]

Un fan d'arithmétique Ben ?

Entre autre...
Comme pas mal de (vieux) matheux, j'ai une prédilection pour l'arithmétique et la géométrie dont les énoncés sont souvent extrêmement élémentaires (quand on est vieux, on a plus de mal avec les trucs compliqués...)

[paquito]

[quote="Ben314"]Je sais pas si, comme le dit paquito, elle "présente beaucoup trop de difficultés", mais par contre, ce que je vois, c'est que telle qu'elle elle me semble "bien fausse" et ça sent la recopie d'une preuve correcte par quelqu'un qui n'a pas compris la preuve.

Si on suis la preuve, on part d'une solution et on en fabrique une nouvelle de la forme où [SIZE=4][U]01, mais si notre cercle contient de tels points, l'ensemble des dénominateurs est une partie non vide de N qui admet donc un plus petit élément, et en partant de cette solution minimale, la démonstration devient claire.
Reste qu'il y a encore beaucoup de calcul, mais ça doit quand même être à la portée d'un TS spé maths. Sinon, je n'ai pas beaucoup vu d'arithmétique dans cette démonstration...

PS: en prenant x²+y²=1, P(4/5; 3/5) et P'(1; 1), on obtient Q(0; -1), ce qui est normal.