Tangente commune et exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 20:52
par Guiguidu60 » 08 Nov 2012, 20:52
Bonjour,
J'ai un problème ouvert à faire pour jeudi prochain mais je n'y arrive pas.
J'ai déjà fais la figure sur un logiciel de géométrie et j'ai conjecturer qu'il en existe une.
Mais je n'arrive pas à le démontrer.
Voici l'énoncé :
Existe-t-il une (des) tangente(s) commune(s) aux courbes C et C' d'équation y=exp(x) et y= - exp (-x-1) ?
Si oui, en donner une équation.
Merci pour votre aide
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 21:08
par bentaarito » 08 Nov 2012, 21:08
Commence par écrire le système que tu cherches à résoudre pour voir
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 21:12
par Guiguidu60 » 08 Nov 2012, 21:12
Oui mais je ne vois pas exactement quel système résoudre
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 21:15
par bentaarito » 08 Nov 2012, 21:15
écris les équations d'une tangente à la courbe de chacune des deux fonctions
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 21:28
par Guiguidu60 » 08 Nov 2012, 21:28
J'obtient :
exp(x) (x-a) + exp(x)
et
exp(-x-1) (x-a) - exp(-x-1)
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 21:36
par bentaarito » 08 Nov 2012, 21:36
Guiguidu60 a écrit:J'obtient :
exp(x) (x-a) + exp(x)
et
exp(-x-1) (x-a) - exp(-x-1)
faux!
déjà pour être rigoureux , ça ce n'est en rien une équation, c'est juste une formule qui veut pas dire grand chose
tu dois écrire :
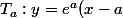+e^a)
et pour la deuxième
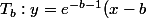-e^{-b-1})
J'ai choisi a et b qui sont pas forcement égaux !raison de plus que les courbes ne s'intersectent jamais
maintenant quand est ce que deux droites sont égales ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Nov 2012, 21:48
par chan79 » 08 Nov 2012, 21:48
Guiguidu60 a écrit:Bonjour,
J'ai un problème ouvert à faire pour jeudi prochain mais je n'y arrive pas.
J'ai déjà fais la figure sur un logiciel de géométrie et j'ai conjecturer qu'il en existe une.
Mais je n'arrive pas à le démontrer.
Voici l'énoncé :
Existe-t-il une (des) tangente(s) commune(s) aux courbes C et C' d'équation y=exp(x) et y= - exp (-x-1) ?
Si oui, en donner une équation.
Merci pour votre aide
Slt
Tu peux montrer que les coubes C et C' sont symétriques par rapport au point (-1/2,0)
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 22:04
par Guiguidu60 » 08 Nov 2012, 22:04
bentaarito a écrit:faux!
déjà pour être rigoureux , ça ce n'est en rien une équation, c'est juste une formule qui veut pas dire grand chose
tu dois écrire :
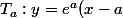+e^a)
et pour la deuxième
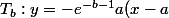+e^{-b-1})
J'ai choisi a et b qui sont pas forcement égaux !raison de plus que les courbes ne s'intersectent jamais
maintenant quand est ce que deux droites sont égales ?
je comprends pas bien la deuxième équation avec les a et b
Mais sinon après il suffit de résoudre Ta=Tb
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 22:07
par Guiguidu60 » 08 Nov 2012, 22:07
chan79 a écrit:Slt
Tu peux montrer que les coubes C et C' sont symétriques par rapport au point (-1/2,0)
Comment fais-tu pour montrer que deux courbe sont symétriques ?
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 22:14
par bentaarito » 08 Nov 2012, 22:14
Guiguidu60 a écrit:je comprends pas bien la deuxième équation avec les a et b
Mais sinon après il suffit de résoudre Ta=Tb
désolé c'était une erreur de ma part en faisant copier/coller, j ai corrigé
et comment comptes tu résoudre ça?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Nov 2012, 22:18
par chan79 » 08 Nov 2012, 22:18
Guiguidu60 a écrit:Comment fais-tu pour montrer que deux courbe sont symétriques ?
Soit M(x,

) un point de C
Son symétrique par rapport à (-1/2,0) est M'(-1-x, -

)
Vérifie que M' est un point de C'
Montre que la tangente commune doit passer par (-1/2,0)
Tu dois trouver y=
)
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 22:38
par Guiguidu60 » 08 Nov 2012, 22:38
bentaarito a écrit:et comment comptes tu résoudre ça?
On remplace par les expressions trouvées
exp(a)*(x-a) + exp(a) = - exp(-b-1) (x-b) + exp(-b-1)
exp(a)*x-exp(a)*a + exp(a) = - exp (-b-1)*x - exp(-b-1)*-b + exp(-b-1)
exp(a)*(x-a+1)=exp(-b-1)*(-x+b+1)
Mais après :mur:
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 22:50
par bentaarito » 08 Nov 2012, 22:50
Guiguidu60 a écrit:On remplace par les expressions trouvées
exp(a)*(x-a) + exp(a) = - exp(-b-1) (x-b) + exp(-b-1)
exp(a)*x-exp(a)*a + exp(a) = - exp (-b-1)*x - exp(-b-1)*-b + exp(-b-1)
exp(a)*(x-a+1)=exp(-b-1)*(-x+b-1)
Mais après :mur:
Non!
deux droites sont égales ( confondues ) si elle s ont même coef directeur et qu'elles ont un point commun
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 22:52
par bentaarito » 08 Nov 2012, 22:52
chan79 a écrit:Soit M(x,

) un point de C
Son symétrique par rapport à (-1/2,0) est M'(-1-x, -

)
Vérifie que M' est un point de C'
Montre que la tangente commune doit passer par (-1/2,0)
Tu dois trouver y=
)
c'est pas plutôt
)
?
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 22:59
par Guiguidu60 » 08 Nov 2012, 22:59
bentaarito a écrit:Non!
deux droites sont égales ( confondues ) si elle s ont même coef directeur et qu'elles ont un point commun
C'est là qu'intervient le système
Il faut que :
exp(a)=-exp(-b-1)
exp(a)=exp(-b-1)
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 23:00
par bentaarito » 08 Nov 2012, 23:00
Guiguidu60 a écrit:C'est là qu'intervient le système
Il faut que :
exp(a)=-exp(-b-1)
exp(a)=exp(-b-1)
je comprends pas ton système
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 23:07
par Guiguidu60 » 08 Nov 2012, 23:07
bentaarito a écrit:je comprends pas ton système
la première égalité correspond aux deux coefficient directeur des tangentes Ta et Tb
la deuxième égalité correspond aux deux points qui doivent être égaux
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 23:08
par bentaarito » 08 Nov 2012, 23:08
égalise les coef dir des deux tangentes puis remplace dans une et égalise les ordonnées à l'origine ça te donne ton a ( et ton b )
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 23:09
par bentaarito » 08 Nov 2012, 23:09
Guiguidu60 a écrit:la première égalité correspond aux deux coefficient directeur des tangentes Ta et Tb
la deuxième égalité correspond aux deux points qui doivent être égaux
attention! c'est pas les bons coef dir! j'ai corrigé dans mon post
et non pour la 2eme! on égalise pas les images des points comme ça
-
Guiguidu60
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Nov 2012, 20:41
-
 par Guiguidu60 » 08 Nov 2012, 23:13
par Guiguidu60 » 08 Nov 2012, 23:13
bentaarito a écrit:attention! c'est pas les bons coef dir! j'ai corrigé dans mon post
et non pour la 2eme! on égalise pas les images des points comme ça
je vois pas trop ce que tu veux dire
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
