Bonjour
Etant donné un système de n équations congruence à une inconnue:
Ai*x=Bi[Ni]
Avant la résolution, que faut-il vérifier ?
Si pour i donné pgcd(Ai,Ni) divise Bi
Si pour i donné Ai est inversible modulo Ni
ou bien y a t-il d'autres conditions ?
Merci pour des réponses
Systeme d'équations congruences
9 messages
- Page 1 sur 1
Re: systeme d'équations congruences
Salut,
Je ne sais si ça va t'aider mais voilà un peu de doc :
https://fr.wikipedia.org/wiki/Th%C3%A9o ... es_chinois
Je ne sais si ça va t'aider mais voilà un peu de doc :
https://fr.wikipedia.org/wiki/Th%C3%A9o ... es_chinois
Re: systeme d'équations congruences
Merci pour ta réponse.
La méthode des restes chinois s'utilise lorsque les Ai sont égaux à 1.
Mais lorsque les Ai sont différents de 1, je pense que :
Si pour i donné pgcd(Ai,Ni) divise Bi alors il y a des solutions, mais je ne garantis rien.
J'ai posté sur plusieurs forums mais aucune réponse!
La méthode des restes chinois s'utilise lorsque les Ai sont égaux à 1.
Mais lorsque les Ai sont différents de 1, je pense que :
Si pour i donné pgcd(Ai,Ni) divise Bi alors il y a des solutions, mais je ne garantis rien.
J'ai posté sur plusieurs forums mais aucune réponse!
Re: systeme d'équations congruences
Bonjour
Tu as un système de N équations avec une seule inconnue (dans Z je suppose), donc facile à résoudre. Mais ta question se situe dans un cadre général avec une question bien étrange :
"Que doit-on vérifier avant de résoudre? " Et bien franchement je vois pas trop.
A la limite cela serait de dire que si une des équations n'a pas de solutions et bien c'est pas la peine de se fatiguer à résoudre les autres!
Sinon tu résous chaque équation, tu notes S_i l'ensemble des solutions (ds Z) de la ième équation. La solution du système est l'intersection des S_i.
Maintenant que veux tu qu'on envisage chaque situation possible? Je vois pas l'intérêt.
Perso ça ne m'étonne pas que tu obtiens aucune réponse pour ce genre de question. C'est pas parce que c'est difficile mais pour les motifs que je viens de dire ci-dessus.
Tu as un système de N équations avec une seule inconnue (dans Z je suppose), donc facile à résoudre. Mais ta question se situe dans un cadre général avec une question bien étrange :
"Que doit-on vérifier avant de résoudre? " Et bien franchement je vois pas trop.
A la limite cela serait de dire que si une des équations n'a pas de solutions et bien c'est pas la peine de se fatiguer à résoudre les autres!
Sinon tu résous chaque équation, tu notes S_i l'ensemble des solutions (ds Z) de la ième équation. La solution du système est l'intersection des S_i.
Maintenant que veux tu qu'on envisage chaque situation possible? Je vois pas l'intérêt.
Perso ça ne m'étonne pas que tu obtiens aucune réponse pour ce genre de question. C'est pas parce que c'est difficile mais pour les motifs que je viens de dire ci-dessus.
Re: systeme d'équations congruences
A la limite cela serait de dire que si une des équations n'a pas de solutions et bien c'est pas la peine de se fatiguer à résoudre les autres!
Oui !
Peut être je me suis mal exprimé. J'aurai dû dire:
A quelles conditions le système admet des solutions ou quelque chose comme ça, mais je ne suis pas trop matheux!
Mais quand même j'ai écrit ça:
Si pour i donné pgcd(Ai,Ni) divise Bi
Maintenant que tu as compris ce que je voulais dire, est ce que c'est la seule condition ou on dois ajouter:
Si pour i donné Ai est inversible modulo Ni
Re: systeme d'équations congruences
**supprimé**
Modifié en dernier par aviateur le 13 Jan 2019, 12:38, modifié 1 fois.
Re: systeme d'équations congruences
Qu'est ce j'ai raconté! Je devais pas être clair. Je supprime donc.
Re: systeme d'équations congruences
Salut,
Ensuite,
- Ta première condition, elle est évidement nécessaire vu que si tu as et que
et que  divise
divise  et
et 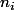 il doit bien évidement diviser
il doit bien évidement diviser  .
.
- Par contre ta deuxième condition n'est pas du tout nécessaire. Par exemple l'équation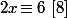 admet évidement des solutions (par exemple
admet évidement des solutions (par exemple 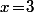 ) alors que 2 n'est pas inversible modulo 8.
) alors que 2 n'est pas inversible modulo 8.
Par contre le truc qui est vrai, c'est que, vu la première condition, si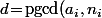) est différent de 1, il doit forcément diviser
est différent de 1, il doit forcément diviser  sinon il n'y a pas de solutions.
sinon il n'y a pas de solutions.
Et s'il divise effectivement alors on a évidement
alors on a évidement 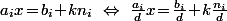 où maintenant
où maintenant 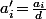 et
et 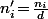 sont premiers entre eux donc
sont premiers entre eux donc 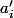 est inversible modulo
est inversible modulo 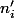 .
.
Bref, on peut se ramener au cas où est inversible modulo
est inversible modulo 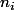 , mais ce n'est pas forcément vrai au départ.
, mais ce n'est pas forcément vrai au départ.
- Il manque on ne peut plus clairement des conditions pour garantir que ton système ait des solutions : là tu ne regarde que les équations que une par une et ça ne risque pas de suffire. Par exemple il est évident les deux équations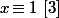 et
et 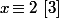 ont toute les deux des solution et il est tout aussi évident que le système formé des deux équations n'en a pas.
ont toute les deux des solution et il est tout aussi évident que le système formé des deux équations n'en a pas.
Enfin et pour terminer, un fois que, pour chaque équation tu as calculé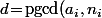) , vérifié qu'il divise bien
, vérifié qu'il divise bien  puis divisé
puis divisé  ,
,  et
et 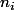 par
par  alors le "nouveau"
alors le "nouveau"  est premier avec le "nouveau"
est premier avec le "nouveau" 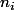 donc inversible modulo
donc inversible modulo 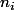 et tu connaît même déjà son inverse vu que pour calculer
et tu connaît même déjà son inverse vu que pour calculer ) tu as forcément appliqué l'algo. d'Euclide qui justement te donne cet inverse. Donc tu n'a aucun problème pour récrire ton équation sous la forme
tu as forcément appliqué l'algo. d'Euclide qui justement te donne cet inverse. Donc tu n'a aucun problème pour récrire ton équation sous la forme 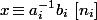 et donc pour te retrouver très exactement dans le cas de figure "classique" du théorème des restes chinois (et c'est bien sûr du fait que toute équation de congruence du premier degré se ramène on ne peut plus facilement à du
et donc pour te retrouver très exactement dans le cas de figure "classique" du théorème des restes chinois (et c'est bien sûr du fait que toute équation de congruence du premier degré se ramène on ne peut plus facilement à du 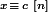 que le théorème des restes chinois n'est énoncé que dans ce cadre là)
que le théorème des restes chinois n'est énoncé que dans ce cadre là)
Déjà, je suppose que ce que tu veut dire, c'est pas "pour i donné", mais "pour tout i" (si tu regarde qu'un seul i parmi toutes tes équations, ben c'est sûr que ça risque pas d'être suffisant !!!)kadaid a écrit:Etant donné un système de n équations congruence à une inconnue:
Ai*x=Bi[Ni]
Avant la résolution, que faut-il vérifier ?
Si pour i donné pgcd(Ai,Ni) divise Bi
Si pour i donné Ai est inversible modulo Ni
Ensuite,
- Ta première condition, elle est évidement nécessaire vu que si tu as
- Par contre ta deuxième condition n'est pas du tout nécessaire. Par exemple l'équation
Par contre le truc qui est vrai, c'est que, vu la première condition, si
Et s'il divise effectivement
Bref, on peut se ramener au cas où
- Il manque on ne peut plus clairement des conditions pour garantir que ton système ait des solutions : là tu ne regarde que les équations que une par une et ça ne risque pas de suffire. Par exemple il est évident les deux équations
Enfin et pour terminer, un fois que, pour chaque équation tu as calculé
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
