bonjour à tous,
je tente désespérément d'aider mon frère à comprendre un exo sur les système d'équation mais j'avoue que je n'y comprend rien et du coup je ne peux pas lui expliquer quelqu'un pourrait-il m'aider?
y=4x au carré -16
y=30x
on demande de choisir parmi trois solutions la bonne et de justifier: on propose (6;128), (7;210) et (8;240).
La bonne réponse est la dernière mais je ne parviens pas à comprendre comment on y arrive. je commence par 30x= 4x au carré -16 et après j'ai fait divers essais avec racines carrées, développement d'identité remarquable et tout et tout mais je n'arrive jamais au bon résultat.
Merci de me mettre sur la piste.
Systeme d'équation à deux inconnues avec un carré
11 messages
- Page 1 sur 1
Salut,
Première méthode :
Tu prends les trois solutions, tu les remplaces dans tes équations et tu ne devrais avoir qu'une des trois solutions qui marchent.
Deuxième méthode : (vraiment plus drôle)
Tu résous le système.
Et parmi la (ou les) solution (s), tu prends celle qui te plait.
Un peu d'explication pour la deuxième méthode :
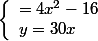
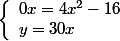
Et dans la première équation, tu retrouves une belle équation à résoudre Bon courage.
Bon courage.
Première méthode :
Tu prends les trois solutions, tu les remplaces dans tes équations et tu ne devrais avoir qu'une des trois solutions qui marchent.
Deuxième méthode : (vraiment plus drôle)
Tu résous le système.
Et parmi la (ou les) solution (s), tu prends celle qui te plait.
Un peu d'explication pour la deuxième méthode :
Et dans la première équation, tu retrouves une belle équation à résoudre
bon je vais peut-être paraître idiote mais j'ai fait un bac L il y a maintenant presque 10 ans et le niveau était vraiment ras des pâquerettes alors un discriminant je connais pas désolé. après recherche apparemment c'est quand c'est égale à 0. on aurait alors 4x au carré -30x -16= 0 mais après on fait comment? un petit cours avec un autre exemple me ferait du bien.
Salut,
On va refaire un petit cours (en live) sur les équations du second degré.
Équation du second degré :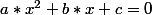 (avec a;)0)
(avec a;)0)
Polynôme (Trinôme) du second degré :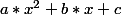 (avec a;)0)
(avec a;)0)
Objectif :
- Déterminer les solutions si elles existent d'une équation du second degré. Dans le cas du trinôme, on parle de racine et non de solution.
Démonstration :
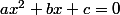
- a;)0, on peut donc factoriser et simplifier par a.
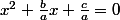
- On remarque ici le début d'un carré parfait :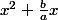
^2 + \frac{c}{a} - \frac{b^2}{4a^2} = 0)
^2 - \frac{b^2 - 4ac}{4a^2} = 0)
Posons :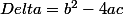 (appelé le discriminant)
(appelé le discriminant)
Discussion sur le signe du discriminant :
Premier cas : Delta Cette somme ne peut donc pas s'annuler. Il n'y a pas de solution réelle à cette équation.
[u]Deuxième cas : Delta = 0
L'équation devient alors :^2 = 0)
=> L'équation admet donc une solution (double) :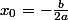
Troisième cas : Delta > 0
On peut donc utiliser une identité remarquable :(a+b))
L'équation devient alors :
^2 - (\frac{sqrt(Delta)}{2a} )^2 =0)
}{2a}) (x + \frac{b}{2a} + \frac{sqrt(Delta)}{2a}) =0)
 (x - \frac{-b-delta}{2a}) =0)
=> Les solutions sont donc :
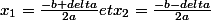
On va refaire un petit cours (en live) sur les équations du second degré.
Équation du second degré :
Polynôme (Trinôme) du second degré :
Objectif :
- Déterminer les solutions si elles existent d'une équation du second degré. Dans le cas du trinôme, on parle de racine et non de solution.
Démonstration :
- a;)0, on peut donc factoriser et simplifier par a.
- On remarque ici le début d'un carré parfait :
Posons :
Discussion sur le signe du discriminant :
Premier cas : Delta Cette somme ne peut donc pas s'annuler. Il n'y a pas de solution réelle à cette équation.
[u]Deuxième cas : Delta = 0
L'équation devient alors :
=> L'équation admet donc une solution (double) :
Troisième cas : Delta > 0
On peut donc utiliser une identité remarquable :
L'équation devient alors :
=> Les solutions sont donc :
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
