Bonjour tout le monde =)
J'ai un petit exercice de DM qui n'est pas des plus faciles. Je viens de finir la première partie qui concerne la fonction et j'aimerais savoir si elle est bonne avant d'attaquer la seconde ^^'
----
Soit

un réel strictement positif.
On nomme
)
la fonction défine sur

pour tout

réel positif par :
 = \frac{x(a+1) + a}{x+a})
Dans la première question on veut montrer que
 = x)
admet une unique solution appelée
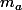
dans

Mon idée est d'appliquer le théorème de la bijection. Dans un premier temps je vais montrer que la fonction
)
est continue sur

puis dans un second temps je montrerai qu'elle est strictement monotone sur

i) Continuité.
La fonction
)
est un rapport de polynômes de degré un et d'incconue

, elle est donc une fonction rationnelle. On en déduit qu'elle est continue sur son ensemble de définition, c'est-à-dire

De plus, on a
 = \mathbb{R}_+)
ii) Dérivabilité.
Dans cette partie on va d'abord calculer la dérivée
)
de la fonction
)
On rappelle que

et

sont des réels positifs et que

est différent de 0. On étudiera ensuite le signe de cette dérivée pour conclure sur la stricte monotonie de la fonction.
On a :
 = \frac{(xa+x+a)'(x+a) - (xa+x+a)}{(x+a)^2} \\ <br /><br />\Rightarrow f'_a(x) = \frac{(a+1)(x+a) - [x(a+1)+a)]}{(x+a)^2} \\<br /><br />\Rightarrow f'_a(x) = \frac{(a+1)(x+a)-x(a+1)-a}{(x+a)^2} \\<br /><br />\Rightarrow f'_a(x) = \frac{(a+1)(x+a)}{(x+a)^2} - \frac{x(a+1)+a}{(x+a)^2} \\<br /><br />\Rightarrow f'_a(x) = \frac{(a+1)}{(x+a)} - \frac{x(a+1)+a}{(x+a)^2})
Or, on a
}{(x+a)} \geq 0)
et
^2 \geq 0)
et
x+a \geq 0)
Vérifions que
 \geq 0 \Leftrightarrow \frac{a+1}{a+x} \geq \frac{(a+1)x+a}{a+x})
Les conditions sur

et

rendent possibles les opérations suivantes :
x+a}{a+x} \\<br /><br />\Rightarrow (a+1)(a+x) \geq (a+1)x+a \\<br /><br />\Rightarrow a+x \geq x + \frac{a}{a+1} \\<br /><br />\Rightarrow a - \frac{a}{a+1} \geq 0 \\<br /><br />\Rightarrow \frac{a^2}{a+1} \geq 0)
Cette dernière inégalité est vraie pour tout

réel strictement positif.
On en déduit donc que
 \geq 0)
pour tout x réel positif et pour tout a réel strictement positif. D'après le Principe de Lagrange,

est strictement croissante sur

Conclusion : on déduit d'après le théorème de la bijection que
 = x)
admet une unique solution
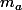
dans

--
La seconde question demande de résoudre l'inéquation
 \geq x)
pour tout

réel positif.
On note que :
 \geq x \Leftrightarrow \frac{x(a+1)+a}{x+a} - x \geq 0)
Soit :
+a}{x+a} - x \geq 0 \Rightarrow \frac{x[(a+1)-(x+a)]+a}{x+a} \geq 0 \\<br /><br />\Rightarrow \frac{x(1-x) + a}{x+a} \geq 0)
Or, on a

et

strictement positif donc le signe de l'expression dépend de celui de
)
On pose
 = x(1-x))
polynôme du second degré d'incconue

. Les deux racines réelles de ce polynôme sont 0 et 1. On en déduit que

est positif pour

compris entre 0 et 1 d'après la règle du signe du trinôme.
De facto,
 \geq x \Rightarrow 0 \leq x \leq 1)
---
La troisième question demande de donner le tableau de variation de
)
D'après la première question, elle est strictement croissante sur son ensemble de définition.
Dois-je calculer les limites ? Flemme... (a)
----
Voilà pour le moment

Enjoy =P Et merci

