Symbole environ inférieur ou égal

[Pseuda]

Bonjour,

Existe-t-il un symbole mathématique qui signifie : "inférieur ou égal à une valeur approchée", ou "environ inférieur ou égal à", comme il en existe un pour "environ égal à" : ?
Par exemple, , soit (car ).

[Ben314]

Salut,
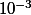
Pas à ma connaissance, mais faut aussi dire que si tu sait par exemple que à près ben tu en déduit la "vrai" inégalité donc je vois pas bien quel intérêt pourrait avoir un "approximativement plus petit que".

[fatal_error]

hello ben,

je présume que c'est pour dire environ égal avec la notion que c'est inférieur (genre proche mais par en dessous)

[titine]

Bonjour,

Existe-t-il un symbole mathématique qui signifie : "inférieur ou égal à une valeur approchée", ou "environ inférieur ou égal à", comme il en existe un pour "environ égal à" : ?
Par exemple, , soit (car ).

3√3 ≈ 5,196152
Donc :
5 < 3√3 < 6
et 5,1 < 3√3 < 5,2
et 5,19 < 3√3 < 5,20
et 5,196 < 3√3 < 5,197
...
Si x ≤ 3√3 on ne peut pas affirmer que x ≤ 5,196 car 3√3 est plus grand que 5,196.
Par contre on peut affirmer que x < 5,197 car x≤ 3√3 < 5,197

[Pseuda]

Salut,
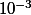
Pas à ma connaissance, mais faut aussi dire que si tu sait par exemple que à près ben tu en déduit la "vrai" inégalité donc je vois pas bien quel intérêt pourrait avoir un "approximativement plus petit que".

Bonsoir,

Ce serait pour répondre à des questions du genre : "à partir de quelle quantité de ...., à partir de quel volume .... de la sphère ..., jusqu'à quel poids de .... ", bref une question tirée (par les cheveux) de la vie courante, résultat d'un calcul qui s'exprime dans une certaine unité (kg, litre, m²).
On exprime le résultat sous forme décimale (car cela n'aurait pas beaucoup de sens de l'exprimer sous forme exacte avec des ou des ).