Suites (TS)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Julius
- Membre Naturel
- Messages: 29
- Enregistré le: 01 Nov 2006, 11:24
-
 par Julius » 23 Jan 2007, 19:00
par Julius » 23 Jan 2007, 19:00
Bonsoir à tou(te)s.
Voilà j'ai un "petit" problème sur les suites que je ne parviens par à résoudre...
Soit (Un) la suite définie par U0= 1
U1=

U(n+2)= U(n+1) + Un
Démontrer que Un=

Si quelqu'un pouvait m'aider... :fr: Merci d'avance.

EDIT : oups désolé pour l'affichage je change cela de suite!
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 23 Jan 2007, 19:30
par Quidam » 23 Jan 2007, 19:30
Fais une démonstration par récurrence !
-
Julius
- Membre Naturel
- Messages: 29
- Enregistré le: 01 Nov 2006, 11:24
-
 par Julius » 23 Jan 2007, 19:36
par Julius » 23 Jan 2007, 19:36
Merci de ta réponse mais vu qu'on ne connaitque U(n+2), comment faire? :s
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 23 Jan 2007, 19:40
par Quidam » 23 Jan 2007, 19:40
Julius a écrit:Merci de ta réponse mais vu qu'on ne connaitque U(n+2), comment faire? :s
Tu supposes que
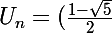^n)
et que :
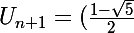^{n+1})
... et tu essaie de démontrer que dans ce cas :
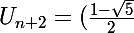^{n+2})
Et ce sera gagné !
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 23 Jan 2007, 19:41
par Joker62 » 23 Jan 2007, 19:41
Utilise la forme généralisée de la récurrence
Suppose la propriété vraie pour tout m inférieur ou égale à n+1 pour un n donné
Calcule U(n+2) = U(n+1) + U(n)
Et calcule ((1-Racine(5))/2)^(n+2) tu trouveras la même choses
-
Julius
- Membre Naturel
- Messages: 29
- Enregistré le: 01 Nov 2006, 11:24
-
 par Julius » 23 Jan 2007, 20:36
par Julius » 23 Jan 2007, 20:36
Merci à vous deux. ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités


