Suites ...

par **mathis** » 28 Nov 2006, 21:30

Bonjour, j'ai un petit probleme ... j'espere que vous pourrez m'aider

u=t+w

t=(19/4)*(1/3^n) w=(6n-15)/4

Calculer Tn , Tn=t0+t1+t2+...+tn
Calculer Wn, Wn=w0+w1+...+wn

En deduir Un=u0+u1+...+un

merci d'avance

par **fred** » 28 Nov 2006, 21:38

mathis a écrit:Bonjour, j'ai un petit probleme ... j'espere que vous pourrez m'aider

u=t+w

t=(19/4)*(1/3^n) w=(6n-15)/4

Calculer Tn , Tn=t0+t1+t2+...+tn
Calculer Wn, Wn=w0+w1+...+wn

En deduir Un=u0+u1+...+un

merci d'avance

Peux tu confirmer

?

par **mathis** » 28 Nov 2006, 21:39

Effectivement c'est bien cela

par **fred** » 28 Nov 2006, 21:45

Alors on peut écrire

Ca ressemble étrangement à la somme d'une suite géométrique de raison...
Pour

,tu fais pareil.Tu développe l'expression pour voir si tu ne reconnais pas la ou les sommes de suites particulières

par **fred** » 28 Nov 2006, 21:57

Tu trouves ???

par **mathis** » 28 Nov 2006, 22:10

Et pour en deduire Un ?

merci

par **mathis** » 30 Nov 2006, 19:29

Personne ne peut m'aider ...

par **Elsa_toup** » 30 Nov 2006, 21:14

Ben c'est logique, non ? Si u=t+w,

...
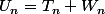
Voilà pourquoi il faut lire les énoncés que l'on recopie ... :lol:

Suites ...

Suites ...

Qui est en ligne