Suites

[EnzoLRG]

Salut, C'est surement tous bete a faire comme execice mais je ne sais pas comment m'y prendre. Help me !!!

2) On considère la suite ( un ) définie pour tout n entier naturel par : un = n² + n
a) Calculer en fonction de n : u indice (n+1) - u indice(n)
b) En déduire le sens de variation de la suite ( u indice (n) )

Merci d'avance.

[Mateo_13]

Bonjour,

2) On considère la suite ( un ) définie pour tout n entier naturel par :
a) Calculer en fonction de n :
b) En déduire le sens de variation de la suite

Pour calculer , il faut que dans la formule de ,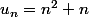
à chaque fois que tu vois la lettre , tu la remplace par .

Donne-nous tes essais de calculs stp.

Cordialement,
--
Mateo.

[annick]

Bonjour,

pour exprimer u(n+1), il faut que tu remplaces tous les n de u(n) par n+1.

[EnzoLRG]

Un = (n+1)² + (n+1)
comme sa ?

[Sa Majesté]

[Mateo_13]

comme ça ?

Il manque le "n+1" dans le membre de gauche :

[EnzoLRG]

ok . Bon, maintenant il faut transformer la suite en fonction,
Sa serai donc : f(x) = (x+1)² + (x+1)

[Mateo_13]

Lis-bien l'énoncé, on ne te dit pas d'étudier le sens de variation de cette fonction,
mais d'étudier le signe de la différence de deux termes consécutifs.

Une remarque : "Sa" dans tes messages, ça s'écrit "Ça", (avec une cédille).

[EnzoLRG]

les deux sont positifs.