Suites

[ch09]

Bonjour, je suis en Terminale ES j'ai prochainement un devoir sur les suites, seulement je ne comprends pas certains points. Par exemple un exercice était le suivant : Soit la suite arithmétique (un) de raison r telle que u10 = 13 et u20 = 14.

La question était : calculer r puis en déduire un en fonction de n, seulement pour exprimer un en fonction de n il me faut u0, or je ne l'ai pas, comment faire dans ce cas? Merci d'avance

[hdci]

Bonjour,

Avant tout, il faut bien connaître la définition d'une suite arithmétique : c'est... ?

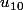En utilisant cette définition, en connaissant la raison , et connaissant , comment calcule-t-on ? ?
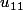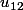Plus généralement, ?

Du coup en utilisant le résultat précédent et en prenant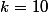 , connaissan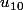t et 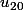, comment trouve-t-on la raison ?

Il n'est nul besoin de connaître finalement. Par contre une fois qu'on a r, avec 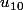on sait calculer , qui vaut... ?

Ce qui permet d'avoir en fonction de

[ch09]

Pour calculer u0 ma formule est : un = u0 + nr mais u0 est inconnu donc je ne vois pas comment faire

[Lostounet]

Pour calculer u0 ma formule est : un = u0 + nr mais u0 est inconnu donc je ne vois pas comment faire

Exprime u10 et u20 en fonction de u0 et R...

Tu obtiens un système de 2 équations à deux inconnnues ...

[ch09]

On a très peu fait de systèmes… mais si je fais ceci :

u10 = u0 + n x r
13 = u0 + 10 x 0,1
13 = u0 + 1
u0 = 13 - 1
u0 = 12

est-ce que cela fonctionne?

[Lostounet]

Euh...tu as inventé une donnée.
Comment tu sais que r=0.1 ?!

On ne connaît ni r ni U0..

On doit écrire U10=u0+10r
Et U13=u0+13r

Donc....
13=u0+10r
14=u0+13r

Un système à deux inconnues u0 et r.
Revois la méthode si tu as oublié, a priori c'est au programme du brevet ....

[Lostounet]

Ah je viens de lire l'énoncé.. ils veulent te faire calculer R d'abord...

À ce moment oui si tu connais R tu calcules u0 facilement.

[ch09]

Pour calculer r j'ai fais : un = up + (n-p) r

[hdci]

Pour en revenir à la défiition.
Tu as écrit qu'une suite arithmétique est donnée par .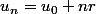

Mais à ma connaissance, ce n'est pas la définition : c'est une conséquence de la définition.

(Bien que formellement on puisse dire que c'est la définition, et donc que "ma définition" est une conséquence de celle-ci...)

Quoi qu'il en soit, tu as forcément vu 2 façons de définir une suite arithmétique. Quelle est l'autre façon ?

(Indice 1 : on dit que c'est une définition par une relation de récurrence)
(Indice 2 : une relation de récurrence simple, c'est une relation qui exprime en fonction de )

[ch09]

Je pense peut être à un+1 = un + r

[hdci]

Oui c'est cela.

Une fois que tu as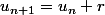 , il n'est pas très difficile de calculer en fonction de .

Il n'y a plus qu'à appliquer à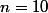 et 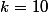: cela donne une équation en et on trouve facilement .

Après quoi on trouve facilement (avec la formule que tu utilisais 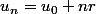appliquée à n=10) et il n'y a plus qu'à conclure.

[ch09]

D'accord merci pour votre réponse!