Suites

[Phymathi]

Bonjour à tous,
Je m'intéresse en particulier à étudier la convergence de la somme des 1/k , k allant de k=1 à k=n
j'ai montré donc que la suite était croissante et que U_2n - U_n > 1/2 (l'énoncé était guidé)
mais après je sais pas comment procéder, sachant que je n'ai pas le droit d'utiliser les suites de Cauchy..
En l'attente d'une réponse, Merci.

[chan79]

salut
Suppose que admette comme limite un réel a.
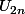
Que dire de et de ?

[aviateur]

Bonjour

Ou alors tu en déduis que

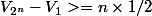
[Phymathi]

salut
Suppose que admette comme limite un réel a.
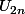
Que dire de et de ?

Bonsoir,
donc la différence doit être égale à 0 ?
Or c'est >=1/2 , donc la suite est divergente ?

[Phymathi]

Bonjour

Ou alors tu en déduis que

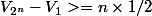
Salut,
On peut pas dire plutot que la suite Un est majorée par n?
Donc Un<n <=> -Un>-n
On a U_2n - Un > 1/2 <=> U_2n - n > 1/2 <=> U_2n > 1/2 + n
On a 1/2 + n tend vers + l'infini , donc la suite est divergente ?

[aviateur]

Salut je ne comprend pas. En tout cas U_{2n}-U_n>{1/2} montre que la suite diverge comme vu ci-dessus.
Mais U_{2n}-U_1>n/2 donne une minoration mais ça ne va pas plus loin.

[Pseuda]

On peut pas dire plutot que la suite Un est majorée par n?
Donc Un<n <=> -Un>-n
On a U_2n - Un > 1/2 <=> U_2n - n > 1/2 <=> U_2n > 1/2 + n
On a 1/2 + n tend vers + l'infini , donc la suite est divergente ?

Bonsoir,

Tu supposes que la suite Un est majorée par n (ne pas oublier : quelque soit n), et tu aboutis à ce qu'elle soit divergente. Donc contradiction, donc Un n'est pas majorée par n quelque soit n, mais cela ne prouve pas qu'elle diverge vers +inf (par exemple Un=(-2)^n).

[Phymathi]

On peut pas dire plutot que la suite Un est majorée par n?
Donc Un<n <=> -Un>-n
On a U_2n - Un > 1/2 <=> U_2n - n > 1/2 <=> U_2n > 1/2 + n
On a 1/2 + n tend vers + l'infini , donc la suite est divergente ?

Bonsoir,

Tu supposes que la suite Un est majorée par n (ne pas oublier : quelque soit n), et tu aboutis à ce qu'elle soit divergente. Donc contradiction, donc Un n'est pas majorée par n quelque soit n, mais cela ne prouve pas qu'elle diverge vers +inf (par exemple Un=(-2)^n).

Bonsoir,
Donc je n'ai pas le droit de dire que :

[Pseuda]

Si, tu peux l'écrire car c'est vrai et tu aboutis à une conclusion vraie, mais cela montre que la suite (U2n) tend vers +inf, mais cela ne montre pas pour la suite (Un). (que fais-tu des termes U2n+1 ?).

Reprends le message de Chan79 plus haut : il démontre que (Un) ne tend pas vers une limite finie. Il faut ajouter autre chose pour conclure.

[Lostounet]

mais cela ne montre pas pour la suite (Un). (que fais-tu des termes U2n+1 ?).

Re,

J'ai pas lu avant mais il me semble que si une suite admet une extraction divergente alors elle est elle-même divergente non?
Donc (U2n) divergente suffit pour montrer que (Un) diverge?

Mais bon au stade où on en est, vaut mieux faire autre chose.

[Pseuda]

Bonjour,

En effet, ceci montre que Un diverge (car si Un convergeait, U2n aussi), mais ne montre pas qu'elle diverge en tendant vers +inf (U2n peut diverger vers +inf sans que Un le fasse, voir exemple plus haut).

Donc si la question est : "montrer que Un diverge", ok ; si la question est : "montrer qu'elle diverge vers +inf" (c'est quand même plus intéressant), pas ok.

En fait, il suffit juste de rajouter que U2n+1=U2n + 1/(2n+1) pour démontrer que (Un) diverge en tendant vers +inf. Pas mal.

[zygomatique]

salut

tout le pb vient des quantificateurs :

pour tout entier n :

donc pour tout entier k :

il suffit alors de faire tendre k vers +oo ...