Bonjour.
La suite (Un) est définie par :
U0 = 5
U(n) = (1 + 2/n) U(n-1) + 6/n
Et la suite (dn) par d(n) = U(n) - U(n-1)
Cette suite (dn) est arithmétique de raison 8 (en fait de manière plus générale la raison est 3+U0)
Pas de problème pour le vérifier avec un tableur mais je n'arrive pas à le démontrer. Pourriez vous m'aider.
Merci.
Suites
7 messages
- Page 1 sur 1
par Sake » 25 Sep 2015, 10:57
sergecroibier a écrit:Bonjour.
La suite (Un) est définie par :
U0 = 5
U(n) = (1 + 2/n) U(n-1) + 6/n
Et la suite (dn) par d(n) = U(n) - U(n-1)
Cette suite (dn) est arithmétique de raison 8 (en fait de manière plus générale la raison est 3+U0)
Pas de problème pour le vérifier avec un tableur mais je n'arrive pas à le démontrer. Pourriez vous m'aider.
Merci.
Bonjour,
Que vaut
par titine » 25 Sep 2015, 11:09
Sake a écrit:Bonjour,
Que vaut?
Il me reste toujours de n et des Un ...
d(n) = 2/n (U(n-1) + 3)
Sauf erreur de calcul ça donne :
d(n+1) - d(n) = [2/(n(n+1))] U(n-1) + 6/(n(n+1))
par sergecroibier » 25 Sep 2015, 11:34
Il me reste toujours de n et des Un ...
d(n) = 2/n (U(n-1) + 3)
Sauf erreur de calcul ça donne :
d(n+1) - d(n) = [2/(n(n+1))] U(n-1) + 6/(n(n+1))
d(n) = 2/n (U(n-1) + 3)
Sauf erreur de calcul ça donne :
d(n+1) - d(n) = [2/(n(n+1))] U(n-1) + 6/(n(n+1))
par chan79 » 25 Sep 2015, 12:54
Après quelques manipulations avec un tableur, on peut conjecturer que d(n)=8(n+1)
et donc aussi que u(n-1)=4n²+4n-3 car d(n)=(2*u(n-1)/n)+6/n
Et u(n-1)=4n²+4n-3 se démontre facilement par récurrence
on a donc u(n)=4n²+12n+5
et donc aussi que u(n-1)=4n²+4n-3 car d(n)=(2*u(n-1)/n)+6/n
Et u(n-1)=4n²+4n-3 se démontre facilement par récurrence
on a donc u(n)=4n²+12n+5
par chan79 » 25 Sep 2015, 19:44
Autre méthode
On suppose)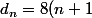
Il faut démontrer)
on a
)
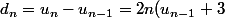(égalité 1)
)
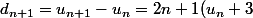(égalité 2)
A partir de l'égalité 1, on a :
(égalité 3)
On transforme maintenant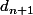
à partir de l'égalité 2 et de la définition de 
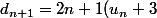=\fra{2}{n+1}\((1+ \fra{2}{n})u_{n-1}+\fra{6}{n}+3\))
on utilise l'égalité 3 et l'hypothèse de récurrence
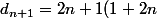(\fra{n8(n+1)}{2}-3)+\fra{6}{n}+3\))
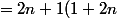(4n^2+4n-3)+\fra{6}{n}+3\))
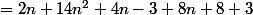=\fra{2}{n+1}(4n^2+12n+8))
)
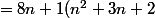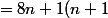(n+2)=8(n+2))
cqfd (reste à vérifier que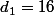
)
trop long par rapport à l'autre méthode ci-dessus
On suppose
Il faut démontrer
on a
A partir de l'égalité 1, on a :
On transforme maintenant
on utilise l'égalité 3 et l'hypothèse de récurrence
cqfd (reste à vérifier que
trop long par rapport à l'autre méthode ci-dessus
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 107 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :