Suites

[mariie98]

Bonjour,
J'ai fait un exercice sur la suite et j'aimerais savoir si ce que j'ai fait jusqu'à maintenant est bon!
"On considère la fonction f définie sur ]- l'infini, 6[ par f(x)= 9/(6-x)
On définit pour tout entier naturel n la suite (Un) par U0=-3 et Un+1=f(Un)"

1a) Demontrer que si x inférieur a 3 alors 9/6-x inférieur à 3
J'ai fait un tableau de variation et j'ai réussi à le démontrer!

b) En déduire que pour tout entier naturel n, Un inférieur à 3
Démonstration par récurrence mais je ne sais pas par ou commencer...

c)Etudier le sens de variation de la suite (Un)
Un inférieur à Un+1 donc
9/(6-Un) inférieur à 9/(6-Un+1)
9(6-Un+1) inférieur à 9(6-Un)
96-9Un+1 inférieur à 96-9Un
-9Un+1/9 inférieur à -9Un/9
Un inférieur à Un+1
La suite Un est croissante

2) On considère la suite (Vn) définie pour tout entier naturel n par Vn=1/Un-3
a) Démontrez que la suite (Vn) est une suite arithmétique de raison -1/3
je n'ai pas réussi
b)Déterminez Vn puis Un en fonction de n
U0=1/0-3 = -1/3
Vn= U0 +nr
Vn=-1/3+n(-1/3)
Vn=1/Un-3
Un=1/(Vn) +3

Merci d'avance

[Ericovitchi]

x -x > - 3 --> 6-x > 3 --> 1/(6-x) 9/(6-x) 0 donc la suite est croissante.

Après, as-tu oublié des parenthèses dans la définition de Vn ?

[maths-lycee fr]

Bonjour,
J'ai fait un exercice sur la suite et j'aimerais savoir si ce que j'ai fait jusqu'à maintenant est bon!
"On considère la fonction f définie sur ]- l'infini, 6[ par f(x)= 9/(6-x)
On définit pour tout entier naturel n la suite (Un) par U0=-3 et Un+1=f(Un)"

1a) Demontrer que si x inférieur a 3 alors 9/6-x inférieur à 3
J'ai fait un tableau de variation et j'ai réussi à le démontrer!

b) En déduire que pour tout entier naturel n, Un inférieur à 3
Démonstration par récurrence mais je ne sais pas par ou commencer...

c)Etudier le sens de variation de la suite (Un)
Un inférieur à Un+1 donc
9/(6-Un) inférieur à 9/(6-Un+1)
9(6-Un+1) inférieur à 9(6-Un)
96-9Un+1 inférieur à 96-9Un
-9Un+1/9 inférieur à -9Un/9
Un inférieur à Un+1
La suite Un est croissante

Revoir les différentes méthodes pour étudier les variations d'une suite
Soit

soit les variations de f avec un=f(n) si un est donnée sous forme explicite

Soit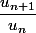 si Un>0

2) On considère la suite (Vn) définie pour tout entier naturel n par Vn=1/Un-3
a) Démontrez que la suite (Vn) est une suite arithmétique de raison -1/3
je n'ai pas réussi

Méthode identique à celle utilisée pour les suites arithmético-géométriques
Je peux vous envoyer une fiche méthode si vous le souhaitez


puis on remplace par son expression en fonction de Un et on veut trouver

b)Déterminez Vn puis Un en fonction de n
U0=1/0-3 = -1/3
Vn= U0 +nr
Vn=-1/3+n(-1/3)
Vn=1/Un-3
Un=1/(Vn) +3