Suites 1èreS: exercice

par **Anonyme** » 16 Mai 2009, 15:54

Bonjour à tous, étant donné que mardi prochain, j'ai un contrôle sur les suites, je m'entraîne à faire quelques exercices (qui je crois seront dans le contrôle). Mais le problème, c'est que je n'arrive pas à tout faire...
Si quelqu'un peut m'aider! Merci d'avance :we:

Voici l'énoncé:
Soit (Un) la suite définie par Un= (2^n) - (5^n)

1)Montrez que pour tout n: U(n+2)= 7U(n+1) - 10U(n)
Celle là je l'ai réussie, donc pas de soucis.

2)Soit (Vn) la suite définie par Vn= U(n+1) - 5U(n). Prouvez que (Vn) est géométrique, puis déterminez sa raison et son premier terme. :hein:

3)Soit (Wn) la suite définie par Wn= -U(n+1) + 2U(n). Prouvez que (Wn) est géométrique, puis déterminez sa raison et son premier terme.

4)Calculez la somme S=Uo + U1 + U2 + ... + U11

Merci à vous!

par **Le Chaton** » 16 Mai 2009, 16:15

Bijour , bijour
tu pourrais essayer de faire

et voir ce que ça te donne .........
Alors pourquoi

? Comprends tu ? Peux tu m'expliquer ? Que vas tu obtenir avec ce calcul ? A quelle(s) condition(s) pourras tu dire que la suite est géométrique ?

par **Anonyme** » 16 Mai 2009, 16:35

V(n+1)/V(n) est la formule pour prouver qu'une suite est géométrique et pour qu'elle soit géométrique il faut obtenir une constante, j'avais d'ailleurs essayé de faire cette méthode, mais je ne suis pas arrivée au bout :hein:
V(n+1)/V(n) = [U(n+1) - 5U(n+1)] / [U(n+1) - 5U(n)] = ...
Je ne sais pas faire :hum:
Can you help me please ! ?

par **Le Chaton** » 16 Mai 2009, 16:44

Alors on a :

Donc

( Tu remplaces ton n par n+1 à chaque fois que tu rencontres un n ... :p )

par **Anonyme** » 16 Mai 2009, 16:46

V(n+1) = [U(n+1)(n+1) - 5U(n+1)] ??

par **Le Chaton** » 16 Mai 2009, 16:49

non
On a

Alors

A chaque fois à la place de n j'ai mis n+1 ...

par **Anonyme** » 16 Mai 2009, 16:56

Haaaa ou!! J'ai beaucoup de mal à voir du premier coup, excuse moi. Donc on obtient:
[U(n+2) - 5U(n+1)] / [U(n+1) - 5U(n)] = 1/1 = 1 =constante
Donc la suite (Vn) est géométrique.

Est-ce que là c'est bon?

par **Le Chaton** » 16 Mai 2009, 17:01

123misslucy a écrit:Haaaa ou!! J'ai beaucoup de mal à voir du premier coup, excuse moi. Donc on obtient:
[U(n+2) - 5U(n+1)] / [U(n+1) - 4U(n)] = 1/1 = 1 =constante
Donc la suite (Vn) est géométrique.

Est-ce que là c'est bon?

Heu ... c'est -5 et pas -4 ..
surement une tite faute de frappe ... mais heu
Tu penses pas qu'après il faille remplacer

Par leur valeur respective? Et après faire un calcul ?

par **Anonyme** » 16 Mai 2009, 17:07

Heu ? je ne vois pas trop comment tout remplacer, ça ferait un calcul infini .. enfin trop long non? Enfin je ne vois pas :triste: help me please ^^

par **Anonyme** » 16 Mai 2009, 17:46

Désolée je dois arrêter maintenant. j'espère que tu pourras me donner quelques info pour la question 4 qui me pose le plus pb, car je n'ai pa vu le cours sur les sommes. Donc voilà. Merci encore pour ton aide, j'espère réussir en entier l'exercice après tout ça.
Bonne fin de journée

par **Le Chaton** » 16 Mai 2009, 17:55

En fait es tu sûre de ta question N°1 ?
C'est

Si c'est bien ça tu peux me montrer comment tu as démontré ça ?

par **Anonyme** » 16 Mai 2009, 21:09

oups, j'ai fais une coquille dans l'énoncé =/

C'est
1)Montrez que pour tout n: U(n+2)= 7U(n+1) - 10U(n)
Ma démonstration est longue et sur ce site j'ai du mal à écrire correctement les termes .. Peux-tu quand même m'aider pour la suite sans ma démonstration ou non ?? =)

par **Maks** » 16 Mai 2009, 21:38

Me voilà. Tu en es où dans l'exercice ?

par **Anonyme** » 16 Mai 2009, 21:44

Je croyais avoir réussi la question 2, mais "Le chaton" m'a dit que c'était faux, enfin j'étais perdu, donc j'en suis à la 2)

par **Maks** » 16 Mai 2009, 21:48

Ok. Bon, comme tu l'as compris, il faut montrer que le rapport

est constant, en d'autres termes, qu'il ne dépend pas de

!

Tu as donc

. Oui ? Il faut que tu calcules cela, et que tu arrives à quelquechose où il n'y a plus de

!

par **Anonyme** » 16 Mai 2009, 21:53

Oui c'est exact, et une fois calculé cela je trouve 1. Mais là je crois que j'ai déliré dans les simplifications !!

par **Maks** » 16 Mai 2009, 21:55

Euh, je n'ai pas fait le calcul. Mais trouver 1 me semblerait étrange. Regarde : cela voudrait dire que

et donc que la suite

serait ... constante !
Attends, je regarde.

par **Maks** » 16 Mai 2009, 22:02

En effet, je ne trouve pas 1 ... mais 2 !
J'ai ça :

, soit

.
Oui ?

par **Anonyme** » 16 Mai 2009, 22:11

Ha! là je vois, bouh par contre avec les simplification ,je vais mettre 3h à trouver 2 comme résultat, mais je te fais confiance, si 2 est le résultat, c'est donc une constante, ainsi la suite (Vn) est géométrique. C'est bien ça?
Maintenant je vais essayer de faire pareil pour la question 3, mais avec le - devant, je vais à tout les coups me tromper XD

par **Maks** » 16 Mai 2009, 22:16

Non, non et re-non, or de question que tu dises que tu ne saches pas faire cette simplification !!
Regarde, c'est tout simple :

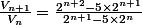, donc

Complète les pointillés. Ensuite, que vaut

?

Je ne te laisserai en aucun cas passer à la suite sans savoir faire ça. Fais moi confiance, ce n'est vraiment pas compliqué (même si ça peut faire peur :ptdr: ). Tu verras, quand tu l'auras fait, tu te sentiras bête ! Et puis, sans te mentir, ce genre de simplification est ultra-classique ! Il FAUT savoir le faire ! Allez, je suis sûr que tu vas y arriver !!

Suites 1èreS: exercice

Suites 1èreS: exercice

Qui est en ligne