Bonjour, tu peux tout d'abord pour plus de lisibilité réécrire les suites
)
et
)
avec des symboles de sommation :
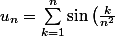})
et

L'encadrement peut être utilisé pour

lorsque

puisque dans ce cas,

. Pour la 2)a), comme tu ne connais pas, à priori, une expression explicite de la somme considérée, tu peux raisonner par récurrence : le cas n=1 étant immédiat, si tu considères un entier n fixé tel que

, alors
^3=1^3+\ldots+n^3+(n+1)^3\leqslant n^4+(n+1)^3)
par hypothèse de récurrence. Il ne reste plus qu'à montrer que
^3\leqslant (n+1)^4)
pour conclure la récurrence. Comme

, alors
^3)
d'où
^3=n\times n^3+(n+1)^3\leqslant n(n+1)^3+(n+1)^3=(n+1)(n+1)^3=(n+1)^4)
. Pour la 2)b), tu peux utiliser l'autre inégalité de (E), à savoir
\geqslant x-\frac{x^3}{6})
valable en particulier pour

pour la même raison qu'en 1). Ainsi,
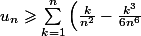})
Or pour

d'où
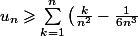=v_n-\frac{1}{6n^2})
Enfin, pour la 3), comme
}{2})
, alors
}{2n^2})
. Si tu essayes de calculer la limite de cette expression, tu as une forme indéterminée de la forme
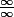
donc il faut factoriser par le terme de plus haut degré, au dénominateur comme au numérateur il s'agit de

donc

et

car

. Enfin en réunissant les inégalités des questions 1) et 2)b), tu as

et comme

alors d'après le théorème des gendarmes,

.

