Bonsoir j'ai un petit problème sur un exercice de maths concernant la suite de Fibbonacci.
Voici une part de l'énoncé:
On considère la suite(Fn)n appartenant à N, définie par F(0)=1; F(1)=1 et F(n+2)=F(n+1)+F(n) quel que soit l'entier naturel n.
On notera que la troisième information signifie que tout terme de la suite, à partir du troisième, est la somme des deux termes qui le précède.
1.Calculer F(2); F(3); F(4) et F(5).
2.Démontrer par récurrence que Fnn quel que soit l'entier naturel n.
Que peut-on en déduire à propos de la suite (Fn)
La première question ne m'a pas posé problème. Cependant la seconde m'a posé quelques soucis au niveau de la justesse de mon raisonnement.
Voici ma réponse:
2.initialisation: au rang 0, F(0)=1supérieur ou égal à 0
Hypothèse de récurrence. Supposons qu'au rang p, p,
F(p) supérieur ou égal à p alors F(p)+1 supérieur ou égal à p+1
Or pour tout p appartenant à N*, F(p+1)=F(p)+F(p-1)
avec Fp-1 supérieur ou égal à 1 puisque F(0)=1; F(1)=1
Ainsi pour tout p appartenant à N* F(p+1) supérieur ou égal à F(p)+1
Donc par transitivité, pour tout p appartenant à N F(p+1) supérieur ou égal à p+1
Ce qui me tracasse ici c'est que j'ai du utilisé le quantifiant * dans mon raisonnement pour démontrer l'inégalité sur . Ce raisonnement est il quand même juste? J'ai entendu parler également de récurrence forte mais je n'en ai jamais utilisé.
Merci d'avance, bonne soirée .
Suite de fibonacci et démonstration par récurrence
7 messages
- Page 1 sur 1
Bonjour, merci pour votre réponse :). J'ai tout de même quelques questions à vous poser:
pourquoi dans l'hypothèse de récurrence supposé vous à partir du rang p supérieur ou égal à 1 et pas pour tout p appartenant à N?
Ne faut il pas supposer également que F(p-1) supérieur ou égal à p-1 (en plus de F(p) supérieur ou égal à p)? Car avec la simple supposition F(p) supérieur ou égal à p j'arrive à F(p)+1 supérieur ou égal à p+1
or F(p+1)-F(p)-1=F(p)+F(p-1)-F(p)-1=F(p-1)-1 et sans supposition sur F(p-1) je ne peux pas conclure sur le signe de la différence (ps: je calcul le signe de la différence pour montrer que F(p+1) supérieur ou égal à F(p)+1 et donc raisonner par transitivité :)).
Merci d'avance :). Bonne journée.
pourquoi dans l'hypothèse de récurrence supposé vous à partir du rang p supérieur ou égal à 1 et pas pour tout p appartenant à N?
Ne faut il pas supposer également que F(p-1) supérieur ou égal à p-1 (en plus de F(p) supérieur ou égal à p)? Car avec la simple supposition F(p) supérieur ou égal à p j'arrive à F(p)+1 supérieur ou égal à p+1
or F(p+1)-F(p)-1=F(p)+F(p-1)-F(p)-1=F(p-1)-1 et sans supposition sur F(p-1) je ne peux pas conclure sur le signe de la différence (ps: je calcul le signe de la différence pour montrer que F(p+1) supérieur ou égal à F(p)+1 et donc raisonner par transitivité :)).
Merci d'avance :). Bonne journée.
Salut.
Dans l'initialisation normalement on a montré que pour n=0 ET n=1 la propriété est vraie c'est-à-dire
\Longrightarrow F(1)) .On part donc de
.On part donc de 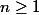 pour montrer l'hérédité.
pour montrer l'hérédité.
Dans les raisonnements classiques,une fois établie F(0) on montre l'hérédité en partant de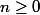 .
.
Dans ton raisonnement tu veux partir de F(p) pour arriver à F(p+1) et dans notre cas ça ne peut pas
marcher car tu as une relation de récurrence entre 3 termes.D'ailleurs je ne vois pas trop la transitivité ici.
Dans ton 1er post tu as écrit "puisque F(p-1) est supérieur à F(1)".Qui te dit que c'est vrai?La suite
est croissante?
J'espère avoir été clair sinon quelqu'un t'expliquera certainement mieux que moi.
Sauf erreur de ma part.
Dans l'initialisation normalement on a montré que pour n=0 ET n=1 la propriété est vraie c'est-à-dire
Dans les raisonnements classiques,une fois établie F(0) on montre l'hérédité en partant de
Dans ton raisonnement tu veux partir de F(p) pour arriver à F(p+1) et dans notre cas ça ne peut pas
marcher car tu as une relation de récurrence entre 3 termes.D'ailleurs je ne vois pas trop la transitivité ici.
Dans ton 1er post tu as écrit "puisque F(p-1) est supérieur à F(1)".Qui te dit que c'est vrai?La suite
est croissante?
J'espère avoir été clair sinon quelqu'un t'expliquera certainement mieux que moi.
Sauf erreur de ma part.
Bonjour merci beaucoup pour votre réponse :). Voici ma transitivité:
je suppose que F(p) supérieur ou égal à p alors F(p)+1 supérieur ou égal à p+1
J'étudie le signe de la différence F(p+1)-F(p)-1= F(p)+F(p-1)-F'p)-1
=F(p-1)-1
C'est pour cela que dans mon raisonnement je doit également partir de la supposition F(p-1) supérieur ou égal à p-1 et initialiser également au rang 2 pour lancer ma proposition au rang 2.
On aurait ainsi pour p supérieur ou égal à 2 F(p-1)-1 supérieur ou égal à 0 ainsi F(p+1) supérieur ou égal à F(p)+1 et donc par transitivité F(p+1) supérieur ou égal à p+1.
C'est pour cela que je vous demandez si il fallait initialiser aussi pour n=2 et supposer aussi F(p-1) supérieur ou égal à p-1 ? ;).
Merci grandement en tout cas pour votre aide :).
ps: peut être qu'une récurrence marche en initialisent juste pour n=0 et n=1 et en supposant simplement que F(p) supérieur ou égal à p mais je ne la vois pas. Ou voulez vous dire qu'il faut partir de la supposition F(p) supérieur ou égal à p et F(p+1)supérieur ou égal à p+1 et montrer que F(p+2) supérieur ou égal à p+2 ?
je suppose que F(p) supérieur ou égal à p alors F(p)+1 supérieur ou égal à p+1
J'étudie le signe de la différence F(p+1)-F(p)-1= F(p)+F(p-1)-F'p)-1
=F(p-1)-1
C'est pour cela que dans mon raisonnement je doit également partir de la supposition F(p-1) supérieur ou égal à p-1 et initialiser également au rang 2 pour lancer ma proposition au rang 2.
On aurait ainsi pour p supérieur ou égal à 2 F(p-1)-1 supérieur ou égal à 0 ainsi F(p+1) supérieur ou égal à F(p)+1 et donc par transitivité F(p+1) supérieur ou égal à p+1.
C'est pour cela que je vous demandez si il fallait initialiser aussi pour n=2 et supposer aussi F(p-1) supérieur ou égal à p-1 ? ;).
Merci grandement en tout cas pour votre aide :).
ps: peut être qu'une récurrence marche en initialisent juste pour n=0 et n=1 et en supposant simplement que F(p) supérieur ou égal à p mais je ne la vois pas. Ou voulez vous dire qu'il faut partir de la supposition F(p) supérieur ou égal à p et F(p+1)supérieur ou égal à p+1 et montrer que F(p+2) supérieur ou égal à p+2 ?
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 121 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
