Somme et factorielle TS

[Sake]

Bonjour
On me demande de démontrer que pour tout n>=1, un=<vn
Sachant que un est une somme (k=0) 1/k! Et vn=un+(1/n*n!)
J'ai décider de raisonner par récurrence mais je suis bloquée a l'hérédité (Pn+1)...
Dans un deuxième temps on me demande de trouver une relation entre (n+1)! et n! et la je ne vois pas du tout :mur:
Bref je suis bloquée avec ces deux questions je ne peux pas avancer plus dans mon exercice...

Merci d'avance de vos réponses !
Bonne journée :lol3:

Salut,

Que vaut v_{n+1} ?

[Sake]

Un+1 + 1/(n+1)*(n+1)!
Est ce que c'est ça ?

fais l'effort d'écrire U_{n+1}. Tel que tu l'écris ici, je lis U_n + 1, c'est-à-dire .

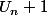
Oui, c'est ça. Et ça, c'est plus grand que quoi ?

[Sake]

Désolé... :/
C'est plus grand que U_n

Oui, mais ça ne nous intéresse pas. Tu voulais montrer que V_{n+1} était plus grand que quoi ?

[Sake]

Que U_(n+1)
Mais U_(n+1) c'est 1/k! Or je ne connais pas k et je ne pense pas que je peux le remplacer par n...

Attends, calme-toi.

On avait montré que V_{n+1} = U_{n+1} + 1/(n+1)*(n+1)!
Et ça, tu vois pas que c'est plus grand que U_{n+1} ?

[Sake]

Ah mais si ! V_(n+1) forcément plus grand que U_(n+1) car V_(n+1) = U_(n+1) + 1/(n+1)*(n+1)! !!

Oui, car 1/(n+1)*(n+1)! est positif

Pour la deuxième question, est-ce que tu peux développer l'écriture de (n+1)! ?

[Sake]

Comment prouver que 1/(n+1)*(n+1)! Est positif ? Dans ma récurrence dois je comparer (n+1)*(n+1)! à n*n! ?

Et c'est la première fois que je vois des factorielles... Le peu que j'ai compris c'est que 5! = 5*4*3*2*1
Donc la (n+1)! = (n+1)*n. ?

Merci pour tes réponses cela m'aide bien !

Ben n est forcément un entier naturel... n+1 est donc positif (sinon même strictement positif mais ce n'est pas important car 0! est défini comme étant 1).

Pas exactement, si tu suis l'exemple de 5!, que vaut n! ?

[Sake]

n ? Euh... Mais n n'a pas de valeur !

C'est pas grave, n c'est n'importe quel entier que tu veux...

Bon, je sens que tu ne sauras jamais à ce train ^^ On peut écrire que n! = n*(n-1)*(n-2)*...*3*2*1
C'est une convention d'écriture, c'est tout. Avec cette définition, on peut facilement écrire la factorielle de tout nombre entier naturel en posant 0!=1.

[Sake]

Donc (n+1)! = (n+1)*n*(n-1)*(n-2)*...*2*1
(Oui désolé je suis un peu lente a comprendre les maths mais une fois que j'ai compris ça le fait ! Vraiment merci !

Pas de problème

Tu peux donc en déduire (n+1)! en fonction de n!

[Sake]

(n+1)! =(n+1)*n!

Très bien )