Bon allez je latexise ma solution :
On part de la formule de Moivre :
 + isin((2n+1)x) = (cos(x) + isin(x))^{2n+1})
On introduit notre dénominateur :
x) + isin((2n+1)x))}{(sin(x)^{2n+1})} = \frac{(cos(x) + isin(x))^{2n+1}}{sin(x)^{2n+1}})
Soit :
 + isin((2n+1)x))}{(sin(x)^{2n+1})} = (\frac{cos(x) + isin(x)}{sin(x)})^{2n+1})
Soit :
 + isin((2n+1)x))}{(sin(x)^{2n+1})} = (cot(x) + i)^{2n+1})
Voilà et donc on a plus qu à déterminer un polynôme Pn(cot(x)²) qui est égal à la partie imaginaire du membre de droite et c'est bon.
Alors on développe grâce à la formule du binôme de Newton :
 + i)^{2n+1} = \displaystyle\sum_{k=0}^{2n+1}C_{2n+1}^{k} (cot(x)^{2n+1-k}) (i^k))
On va distinguer les cas où k est pair et les cas où k impairs. en en effet lorsque k est pair,
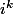
est réel.
On pose j tel que k = 2j+1 et j' tel que k = 2j'
On a :
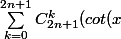^{2n+1-k}) (i^k) = \displaystyle\sum_{j'=0}^{n}C_{2n+1}^{2j'} (cot(x)^{2n+1-2j'}) (i^{2j'}) + \displaystyle\sum_{j=0}^{n}C_{2n+1}^{2j+1} (cot(x)^{2n+1-2j-1}) (i^{2j+1}))
Donc la 2eme somme du membre de droite, i.e ce qui nous intéresse (la première, c'est que du réel donc on en tient pas compte) vaut :
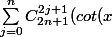^{2n-2j}) (i^{2j+1}))
On peut mettre un i en facteur, il reste i^2j qui se transforme en (-1)^j. On réussit aussi à retrouver notre cot² :zen: : ça fait :
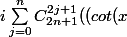^2)^{n-j}) (-1)^j)
Voilà donc on a trouvé ce polynôme :
 = \displaystyle\sum_{j=0}^{n}C_{2n+1}^{2j+1} (X)^{n-j}) (-1)^j)
Qui est tel que :
^2) = \frac{sin((2n+1)x)}{sin(x)^{2n+1}})
Le plus dur pour moi a été d'avoir l'idée de distinguer les valeurs de k, et de pas me tromper dans les valeurs de départ et d'arrivée des différentes sommes.
Maintenant question :
Comment démontre-t-on l'unicité ? :hum:
