Démo Pi²/6 ?

Salut à tous, j'ai un niveau de T°S et je cherche la démonstration de :

lim (n-> +oo) ( 1/1²+1/2²+1/3²+1/4²+1/5²+...+1/n² ) = Pi²/6

Aidez-moi svp :triste:

Oui le grand classique ^^

En TS, ca se démontre pas ^^ Faut passer par les séries de Fourier si je me souviens bien ^^

Dites toujours svp !

Voici un site recensant quatorze preuves du résultat (en anglais).

La onzième est la seule qui peut être comprise d'un bon élève en terminale S, à mon avis.

Bonjour,

il y a aussi la methode suivante qui est accessible en terminale:
Trouver a et b tels que


La somme des se calcule ensuite en remarquant que

Je crois que cette methode est tout a fait faisable en Tale.

uztop a écrit:Je crois que cette methode est tout a fait faisable en Tale.

:++: :++:

Merci pour la quinzième méthode ! :happy2:

Si ça t'intéresse, tu peux aller voir ce poly :

http://clement-boulonne.123.fr/cours/m204.pdf

C'est l'Exemple 3.1.4. (dernier exemple du poly, dernière page)...

il y a un problème dans ton lien (le http apparait deux fois).
Sinon, je ne pense pas que les séries de Fourries soient dans le programme de terminale.

Petite faute de frappe rectifiée :++:

Bonsoir,

SimonB a écrit:La onzième est la seule qui peut être comprise d'un bon élève en terminale S, à mon avis.

Tu sais quelle est la formule de réduction ("By a well-known reduction formula") que l'auteur utilise pour cette 11e démo?

Euler911 a écrit:Tu sais quelle est la formule de réduction ("By a well-known reduction formula") que l'auteur utilise pour cette 11e démo?

Intégration par parties ?

Tu en es sûr? Je n'arrive pas à trouver cette expression de In à partir d'intégrations par parties...:(

uztop a écrit:Bonjour,

il y a aussi la methode suivante qui est accessible en terminale:
Trouver a et b tels que


La somme des se calcule ensuite en remarquant que

Je crois que cette methode est tout a fait faisable en Tale.

Je vois pas comment ut fais pour calculer la somme des In.L integrale qu on obtient me semble assez foireuse a calculer(a la limite,p-e avec un changement de variables,et encore suis pas sur que ca marche)

la somme des est la somme des termes d'une suite geometrique.
Mais il faut bien faire attention, cela ne marche que si a et b ne dependent pas de n. On aura donc deux cas a separer (en fonction de la parite de n)

oui,ca j ai bien compris,mais comment fait tu par exemple pour integrer

c'est explique ici (page 4)
Par contre, j'avoue que c'est un peu plus complique que je ne le pensais (et donc probablement pas faisable en terminale)

Hey,Rieman Lebesgue,pourquoi n y ai je pas pensé?...(bon,p-e car tu as dit que c était niveau Tale lol,mais j aurais du y penser quand meme :marteau: ).Et rn plus,j ai fait partir ma série géométrique de 0 au lieu de 1 :briques:.Sinon,la démo devient quand meme tres simple en utilisant directement Rieman Lebesgue pour les fonctions continues,ya plus a dériver...Et p-e qu on peut arriver a faire la preuve de Riemann Lebesgue pour cette fonction f particuliere au niveau terminale, vu que le seul truc non élémentaire dans Riemann Lebesgue,c est la densité des fonctions C^1 dans les fonctions continues,et que la fonction f en question ici est (probablement) facilement approchable par des fonctions C^1 explicites...

La méthode d'uztop est celle des séries de Fourier, mais il n'y a rien à savoir dessus : on contourne tous les résultats, y compris Riemann-Lebesgue, en faisant des majorations simples. Il faut cependant mettre une borne 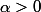à la place de 0 pour l'une de ces majorations (si on veut rester niveau TS). Il reste alors une intégrale de 0 à d'une fonction continue et il faut tout de même savoir qu'une telle fonction atteint ses bornes pour déquiller cette dernière intégrale (seul résultat à admettre niveau TS, et peut-être qu'on peut aussi le contourner).

Euler911 a écrit:Bonsoir,



Tu sais quelle est la formule de réduction ("By a well-known reduction formula") que l'auteur utilise pour cette 11e démo?

Suffit de se souvenir des fameuses intégrales de Wallis je crois...