Bonjour, je ne comprends pas comment trouvé le sens de variation d'une fonction...
Si quelqu'un pouvait m'expliquer comment faire.
Merci.
Sens de variation d'une fonction.
9 messages
- Page 1 sur 1
Eh bah en fait je suis passé en 1ère S sans avoir vu les fonctions carré ni inverse(donc j'ai un peu de mal =$), mais c'est pour savoir le sens de variation de n'importe quel type de fonctions...
Je crois savoir qu'il y a plusieurs méthodes nan?
Une en séparant les fonctions de base enfin du genre 1/x, ax+b...
Je crois savoir qu'il y a plusieurs méthodes nan?
Une en séparant les fonctions de base enfin du genre 1/x, ax+b...
il faut bien comprendre le chapitre important sur le taux de variation...!
c'est simple : la fonction "monte" : elle est croissante et son taux= delta Y/delta x >0
et inversement .
Dy= Yb-Ya ; Dx= Xb-Xa
Sur un graphe c'est évident regardez votre manuel de 1°S
De la on en déduit les dérivées... pas compliqué !!!
La dérivée est >0 la fonction est croissante et inversement ...c'est la traduction du taux de variation...
Qui se conçoit bien s'explique clairement...
c'est simple : la fonction "monte" : elle est croissante et son taux= delta Y/delta x >0
et inversement .
Dy= Yb-Ya ; Dx= Xb-Xa
Sur un graphe c'est évident regardez votre manuel de 1°S
De la on en déduit les dérivées... pas compliqué !!!
La dérivée est >0 la fonction est croissante et inversement ...c'est la traduction du taux de variation...
Qui se conçoit bien s'explique clairement...
cours
[déf] Soit I un intervalle de R non vide (les intervalles sont les parties connexes de R)
une fonction f est strictement croissante sur I si
 \in R^2 \qquad x0) sur I
sur I  strictement croissante sur
strictement croissante sur 
sinon on vérifie
 \in R^2 \qquad x \neq y \Rightarrow \frac{f(y)-f(x)}{y-x}>0)
[rem] une fonction croissante est un "morphisme d'ordre" qui conserve le même
ordre entre les antécédents et leurs images.
exemple: montrons que est décroissante sur R-* et R+*
est décroissante sur R-* et R+*
=\frac{-1}{ab})
si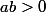 alors
alors
>0)
donc h décroissante sur R+* et R-* et pas sur R* car 1/(-2)<1/2
[déf] Soit I un intervalle de R non vide (les intervalles sont les parties connexes de R)
une fonction f est strictement croissante sur I si
sinon on vérifie
[rem] une fonction croissante est un "morphisme d'ordre" qui conserve le même
ordre entre les antécédents et leurs images.
exemple: montrons que
si
donc h décroissante sur R+* et R-* et pas sur R* car 1/(-2)<1/2
GaRDeLaMe a écrit:Eh bah en fait je suis passé en 1ère S sans avoir vu les fonctions carré ni inverse(donc j'ai un peu de mal =$), mais c'est pour savoir le sens de variation de n'importe quel type de fonctions...
Je crois savoir qu'il y a plusieurs méthodes nan?
Une en séparant les fonctions de base enfin du genre 1/x, ax+b...
Bonjour,
je pense que tu parles des variations des fonctions associées à une fonction f.
par exemple celles de kf, 1/f, racine carrée de f... quand les variations de f sont connues.
Regarde le cours et quelques exemples
Vraiations des fonctions associées à la fonction carré ou valeur absolue
et fonctions associées à la fonction carré
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

