Bonjour j'aurais besoin d'un peu d'aide pour résoudre cette équation :( je viens de finir ma TS )
z² - 2(cosA)z + 1 = 0
mes solutions sont z= cosA(1-i)
= cosA(1+i)
je ne suis pas sur du tout...car il faut disscuter de la valeur de cos²A si celui ci vaut 1 alors Delta est nul .Donc il faut voir deux cas
le premier pour tout Cos²A < 1
le second pour tout Cos²A=1 donc pour A=2pi [ 2pi ]
voila ma démarche ... pourrier vous m'aidez merci beaucoup !
Resolution D'une Equation
7 messages
- Page 1 sur 1
tu es sur de tes solutions?
tu as essayé de remplacer dans l'equation pour vérifier que tu trouves bien 0?
sinon pour ton raisonnement pas la peine de te prendre la tête
tu trouveras des solutions de la formesqrt{\delta}}{2a}) donc si ton
donc si ton  vaut 0 tu retombes bien sur l'expression des solutions dans ce cas :
vaut 0 tu retombes bien sur l'expression des solutions dans ce cas : 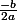 .
.
La solutionsqrt{\delta}}{2a}) est donc également valable pour
est donc également valable pour 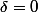
tu as essayé de remplacer dans l'equation pour vérifier que tu trouves bien 0?
sinon pour ton raisonnement pas la peine de te prendre la tête
tu trouveras des solutions de la forme
La solution
nox a écrit:tu es sur de tes solutions?
tu as essayé de remplacer dans l'equation pour vérifier que tu trouves bien 0?
sinon pour ton raisonnement pas la peine de te prendre la tête
tu trouveras des solutions de la formedonc si ton
vaut 0 tu retombes bien sur l'expression des solutions dans ce cas :
.
La solutionest donc également valable pour
je suis pas sur si je me trompe ,mais -b/2a n'est-ce pas la formule a utiliser pour trouver le sommet h(c est a dire x=variable indépendante ) d une parabole???
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :




 et
et 
 et
et 
 ,
,  )
)