TS résolution d'équations de la forme y'=ay+b

[destrukt]

voilà donc c'est l'un des exo d'un dm que je devrais rendre lundi, je m'y prend d'avance;

Soit (E) l'équation différentielle suivante :
(E) y' = -3y + 4e^-2x
1/ Déterminer le réel Lambda tel que la fonction g, définie sur R par g(x) = Lambda e^-2x, soit solution de (E)
2/ Montrer qu'une fonction f est solution de (E) si et seulement si la fonction h=f-g est solution de l'équation différentielle (E') ci dessous.
(E') y' = -3y
3/ résoudre l'équation différentielle (E')
Ma réponse : L'équation différentielle y'=-3y admet comme solutions toute les fonction de la forme f(x) = k e^-3x ou k est un réel.
4/En déduire les solution de l'équation différentielle (E)



voilà je ne sais répondre qu'as la question 3 :hein: si quelqu'un peut m'aider, merci d'avance!

[armor92]

Bonjour destrukt,

Pour le 1) c'est simple, il suffit de remplacer y par lambda * exp(-2x) dans (E).

On applique les règles de dérivation et on obtient une équation en lambda.

Pour le 2) tu démontre l'équivalence :
f est solution de (E)
<=>
h = f - g est solution de (E') (avec g est la solution paticulière de E trouvée dans le 1))

[Quidam]

1) Il suffit de voir ce qui se passe !
Tu supposes que g(x) est solution de (E) ; alors :
g'(x) = -3g(x) + 4e^-2x
Or si , alors , d'où :

soit, en multipliant les deux membres par

... et tu trouves !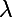

2/ Montrer qu'une fonction f est solution de (E) si et seulement si la fonction h=f-g est solution de l'équation différentielle (E') ci dessous.
(E') y' = -3y
Si on te dit : "montrer que A si et seulement si B", cela veut dire d'une part "montrer que A si B", c'est à dire que si B est vrai alors A l'est aussi (), d'autre part "montrer que A seulement si B", c'est-à-dire que A ne peut être vrai que si B l'est ().

Donc pour montrer "qu'une fonction f est solution de (E) si et seulement si la fonction h=f-g est solution de l'équation différentielle (E')" il faut montrer que si f est solution de E alors h=f-g est solution de E', d'une part, et que réciproquement, si h=f-g est solution de E' alors f est solution de E, d'autre part.

Vas-y !