Résolution équation f(f(x))=x

par **Doraki** » 29 Jan 2010, 16:20

Oui mais est-ce que tu sais trouver les racines d'un polynôme de degré 4 ?

par **Dinozzo13** » 29 Jan 2010, 16:22

Oui ! dois-je le faire ?

par **Doraki** » 29 Jan 2010, 16:25

J'ai mal posé ma question.

Est-ce que ton voisin de classe sait trouver les racines d'un polynôme de degré 4 ?

(et puis sur ton exemple t'as toujours pas fini de calculer ce polynôme)

par **Dinozzo13** » 29 Jan 2010, 16:27

??? :doh: je pense pas pourquoi ?

par **Doraki** » 29 Jan 2010, 16:29

Ben parceque ça sert à rien de résoudre un truc si tu sais pas le faire refaire par ton voisin de classe.
Et puis si tu avais DEPUIS LE DEBUT un moyen de résoudre le problème, pourquoi avoir fait un sujet ?

A ton avis dans quels genre de cas particuliers est-ce qu'il aurait une chance de trouver les racines d'un polynôme de degré 4 ?

par **Dinozzo13** » 29 Jan 2010, 16:32

Doraki a écrit:A ton avis dans quels genre de cas particuliers est-ce qu'il aurait une chance de trouver les racines d'un polynôme de degré 4 ?

J'en sais rien, moi, peut-être

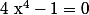
. Mais quel est le rapport avec mon exercice ???

par **Doraki** » 29 Jan 2010, 16:38

Mwais par exemple. Ou quand y'a des racines évidentes.

Le rapport est que en lisant le post #2, ton voisin devrait pouvoir factoriser le poynôme de degré 4.

par **Dinozzo13** » 29 Jan 2010, 16:45

Or si

et

sont deux racine de

donc elles sont aussi des racines de

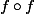
donc par conséquent

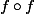
est factorisable par

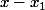
et

par **Doraki** » 29 Jan 2010, 16:50

tu confonds avec f - id et f o f - id.

T'en es où avec f(x) = x²-6x+6 ?

par **Dinozzo13** » 29 Jan 2010, 16:53

Bon ben moi je pige plus rien, reprenons tout à zéro.
on veut résoudre

avec

Mais après que faire et pourquoi ? cest ça que je comprends pas. Parce qu'après tout le reste c'est du chinois pour moi.

par **Skullkid** » 29 Jan 2010, 17:09

Tu cherches les racines de fof - id. Tu sais que les racines de f - id sont racines de fof - id. Donc, tu peux factoriser fof - id par f - id.

Bien entendu, tout ça fonctionne parce que f est un polynôme.

par **Doraki** » 29 Jan 2010, 17:12

Ah pardon, id c'est l'identité : la fonction x -> x.

par **Dinozzo13** » 29 Jan 2010, 17:17

ok, mais ce que je comprends pas, c'est pourquoi ? les racines de f - id sont racines de fof - id ?

par **Doraki** » 29 Jan 2010, 17:22

Oui, comme tu l'as si bien expliqué au post #7

par **Dinozzo13** » 29 Jan 2010, 19:18

donc je fais quoi maintenant ?

par **Doraki** » 30 Jan 2010, 00:34

Ben après tu fais comme t'as dit dans ton post #28

Résolution équation f(f(x))=x

Qui est en ligne