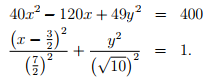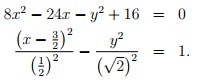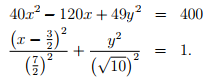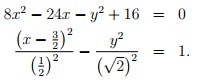Reformer l'équation d'une parabole et d'une hyperbole

[Samathématique]

Bonjour !





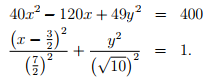
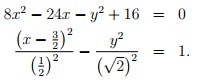
Soit un, l'équation d'une hyperbole
et la deuxième d'une ellipse.
Comment dois-je m'y prendre pour reformer leur équation ? (passer de l'équation 1 à 2)

Merci

[Samathématique]

Encore une p'tite question qui peut vous sembler bête. (Je viens de me mettre à la géométrie analytique)

Soit B le point en (0,1) et M le pointe en (1/2,0)
Pour trouver le coefficient de la droite BM on fait bien 0-1 / 1/2, ce qui donne -2 ?

[chan79]

salut
Divise les deux membres par 40
Ensuite:
(x-3/2)²-9/4+49y²/40=10

...

[pascal16]

40x²-120x+49y²=400
je mets les x ensemble, les y ensemble, je factorise pour avoir les termes au carré avec un coefficient 1
40(x²-3x)+49(y²)=400
forme canonique
40((x-3/2)²-9/4)+49(y²)=400
je passe les constantes à droite, le terme de droite évolue, c'est pour ça qu'on ne divise pas dès le départ habituellement.
40(x-3/2)²+49y²=490
je divise par la constante de droite
(x-3/2)²/(49/4)+y²/10=1
je fais apparaître les carrés en bas
(x-3/2)²/(7/2)²+y²/sqrt(10)²=1

cette méthode s'applique du moment qu'il n'y a pas de terme en "xy", c'est à dire que les axes doivent être verticaux ou horizontaux. Sinon, il faut d'abord trouver le changement de repère puis faire cette méthode, niveau post-bac.

[pascal16]

A(0 ; 0) et B(1/2 ; 1)
tu trouves un coefficient directeur infini pour (BM)
la droite est verticale d'équation x=1/2

[Samathématique]

Merci, j'ai réussi à faire la deuxième équation tout seul

[zygomatique]

salut

personnellement pour me simplifier la vie j'aurai multiplier la première par 10 et la deuxième par 2 ....