Recherche exo sérieux ^^
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Oct 2009, 10:10
par Dinozzo13 » 21 Oct 2009, 10:10
Bonjour, aujourd'hui, j'ai de la peine pour trouver un exercice aussi bien dur qu'intéressant sur les barycentres et tout ce qui concerne déterminer des ensembles à partir d'égalités de normes , quelqu'un en aurait-il ?
P.S. : La présence d'un paramètre dans l'exo ne m'embête aucunement ^^, merci d'avance.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 21 Oct 2009, 10:12
par Timothé Lefebvre » 21 Oct 2009, 10:12
Salut :)
Sur les barycentres ?! J'ai posé un exo appelé "problème physico-mathématique" (cherche dans mes posts) il y a quelques jours. Je n'ai pas encore donné ma solution, tu peux t'y pencher si ça t'intéresse ;)
A +
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Oct 2009, 10:16
par Dinozzo13 » 21 Oct 2009, 10:16
OK, je l'ai trouvé, je vais allé voir ça. J'accepte encore d'autres exos si vous en avez ^^.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 21 Oct 2009, 10:17
par Timothé Lefebvre » 21 Oct 2009, 10:17
Je vais essayer de t'en trouver d'autres alors ;)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Oct 2009, 10:18
par Dinozzo13 » 21 Oct 2009, 10:18
cool ! merci ^^. En attendant, je me penche sur ton exo ^^.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 21 Oct 2009, 10:23
par Timothé Lefebvre » 21 Oct 2009, 10:23
Ok, c'est plus trop dur, j'ai donné tout le raisonnement à mener !
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Oct 2009, 10:24
par Dinozzo13 » 21 Oct 2009, 10:24
j'y suis en ce moment, j'aurai besoin que tu m'aides ^^.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 21 Oct 2009, 10:27
par Timothé Lefebvre » 21 Oct 2009, 10:27
Lol, relis ce que j'ai dit, moi je vais déjeuner et on voit ça après ^^
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 21 Oct 2009, 10:28
par Dinozzo13 » 21 Oct 2009, 10:28
ok, bon ap' :++:
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Oct 2009, 16:34
par Timothé Lefebvre » 23 Oct 2009, 16:34
Salut :)
Je deux exos (DM) assez sympas sur les barycentres et lieux géométriques de 1S, si ça t'intéresse je peux te recopier les énoncés :)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 23 Oct 2009, 17:30
par Dinozzo13 » 23 Oct 2009, 17:30
oui, en effet ça m'intéresse ^^
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Oct 2009, 17:31
par Timothé Lefebvre » 23 Oct 2009, 17:31
Ok :)
Je te les recopie ici avant ce soir.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 23 Oct 2009, 18:38
par Dinozzo13 » 23 Oct 2009, 18:38
ok, merci d'avance ^^
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Oct 2009, 18:43
par Timothé Lefebvre » 23 Oct 2009, 18:43
Je te recopie ça quand ma série est finie ^^
-
mathelot
 par mathelot » 23 Oct 2009, 18:50
par mathelot » 23 Oct 2009, 18:50
bonsoir,
sur les barycentres, calculer les coordonnées barycentriques des points remarquables d'un triangle: G,H,O,I
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Oct 2009, 18:58
par Nightmare » 23 Oct 2009, 18:58
Il est intéressant aussi de remarquer les propriétés liés aux barycentres. Par exemple que dire d'une transformation du plan (ou de l'espace) qui conserve les barycentres?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 23 Oct 2009, 19:01
par Zweig » 23 Oct 2009, 19:01
J'ai un problème sympa sur les barycentres.
Soit
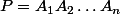
un polygone à

sommets,
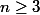
. On associe à ce polygone le polygone
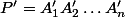
tels que :
[CENTER]
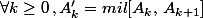
[/CENTER]
On définit alors une suite de polygones par récurrence :
[CENTER]
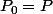
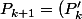,\, \forall k\geq 0)
[/CENTER]
Montrer que chaque sommet de
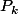
converge vers le centre de gravité de
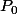
lorsque

tend vers

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 23 Oct 2009, 19:18
par Dinozzo13 » 23 Oct 2009, 19:18
:doh:
Zweig a écrit:J'ai un problème sympa sur les barycentres.
Soit
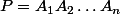
un polygone à

sommets,
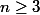
. On associe à ce polygone le polygone
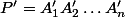
tels que :
[CENTER]
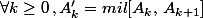
[/CENTER]
On définit alors une suite de polygones par récurrence :
[CENTER]
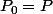
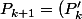,\, \forall k\geq 0)
[/CENTER]
Montrer que chaque sommet de
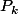
converge vers le centre de gravité de
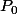
lorsque

tend vers

:doh: alors ça, ça me dépasse
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 23 Oct 2009, 19:52
par Dinozzo13 » 23 Oct 2009, 19:52
Et si on est en Tle S ? :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 116 invités
un polygone à
sommets,
. On associe à ce polygone le polygone
tels que :
[/CENTER]
[/CENTER]
converge vers le centre de gravité de
lorsque
tend vers
