[Défi sérieux S] Polynôme de degré 2009 ^^

[Dinozzo13]

Bonjour ! je vous propose un défi assez sympa je trouve ^^ :

Soit un polynôme de degré .
on a , montrer que

[Dinozzo13]

Mille excuses, je m'étais trompé dans les signes et

[Dinozzo13]

'Y a pas d'amateur ou de matheux

[benekire2]

Donne voir la réponse ^^

[Nightmare]

Salut, j'ai trouvé un truc par récurrence sur le degré, sachant que si P est de degré n+1, le polynôme Q=1/2[P(X)-P(X+1)] est de degré n et vérifie les conditions de l'énoncé.

[Dinozzo13]

Allez, là voilà ^^ :
Moi je résonnerai par récurrence, je ne vois que cela.
Je vais donc démontrer la propriété pour :
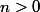
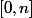
:Si et sur alors on a
Si alors ... .
Supposons que soit vraie, montrons qu'alors si est un polynôme de degré tel que sur . J'applique l'hypotèse de récurrence au polynôme qui est de degré et qui doit vérifier sur .
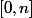
On a ainsi et par conséquent
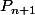
Or , on en déduit donc que est vraie.

[Dinozzo13]

Salut, j'ai trouvé un truc par récurrence sur le degré, sachant que si P est de degré n+1, le polynôme Q=1/2[P(X)-P(X+1)] est de degré n et vérifie les conditions de l'énoncé.

Bien joué :++:

[Nightmare]

Effectivement, après recherche sur internet c'est la solution proposée un peu partout. Dommage je pensais qu'il y avait un truc mieux qu'une récurrence.

[Dinozzo13]

:we: Je suis d'accord, une récurrence c'est pratique des fois, sauf qu'on ne fais que prouver, on ne démontre pas vraiment si tu vois ce que je veux dire.
Bah d'ailleurs quand je suis perdu ou que je ne vois vraiment pas je fais systématiquement un raisonnement par récurrence (Des fois j'en abuse un peu trop je pense ^^)

[Nightmare]

Ce que je veux dire est qu'un raisonnement par récurrence masque souvent le problème.

[Dinozzo13]

oui, en effet je suis d'accord ^^. Mais bon, aux yeux des profs c'est vérifié donc on se contente de ça ^^

[benekire2]

J'aime pas le raisonnement par récurrence, je trouve pas ça très propre, mais bon, ça marche donc a partir de là ...

[Dinozzo13]

:ptdr: on va dire que c'est le joker de la démonstration ^^

[benekire2]

Ouais ^^ En fait je sais même pas exactement ce que je lui reproche ... Mais je ne l'aime pas.