Raisonnement par récurrence.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
kinou56
- Membre Naturel
- Messages: 62
- Enregistré le: 05 Sep 2006, 20:28
-
 par kinou56 » 06 Sep 2006, 17:40
par kinou56 » 06 Sep 2006, 17:40
un petit exo sur le raisonnement par récurrence.
Soit An, le nombre n(n+1)(2n+1)/6 où n appartient N.
1) Calculer A1, A2, A3 (c'est fait)
2) Montrer par récurrence la proposition suivante :
(Pn): An est un entier naturel.
Ayant calculé A1, j'ai trouvé 1 donc P1 est vérifiée.
j'en suis à la deuxième phase : hérédité. Supposons que Pp est vraie, et montrons que Pp+1 est vraie. voilà en cours on s'est arrête là et on doit trouver la suite.
Est-ce qu'il faut calculer Ap. je l'ai fait et j'ai trouvé 2p^3+3p²+1
merci de votre aide.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 06 Sep 2006, 17:47
par Flodelarab » 06 Sep 2006, 17:47
Calcul A(p+1) donc Et regarde si c égal a la somme des carrés jusqu'a n+1
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 06 Sep 2006, 17:59
par nekros » 06 Sep 2006, 17:59
Justement, peut-être ne sait-il pas que la somme des carrés intervient...
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Sep 2006, 18:00
par nada-top » 06 Sep 2006, 18:00
(2n+1)}{6} \in N)
i.e
(2n+1) = 6k)
tel
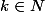
maintenent tu dois prouver que

est vrai pour cela tu dois prouver que

donc
(n+2)(2n+3) = 6k')
tel que

, calcule et tu verra ce que tu trouve en gardant toujours à l'esprit que t'as supposé que
(2n+1) = 6k)
....
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 06 Sep 2006, 18:01
par Flodelarab » 06 Sep 2006, 18:01
Oupps
G lu en diagonale
-
kinou56
- Membre Naturel
- Messages: 62
- Enregistré le: 05 Sep 2006, 20:28
-
 par kinou56 » 06 Sep 2006, 18:02
par kinou56 » 06 Sep 2006, 18:02
ça donne 2p+1^3+3p+1²+1
il suffit de rajouter le petit +1 àcôté du p
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 06 Sep 2006, 18:03
par Flodelarab » 06 Sep 2006, 18:03
kinou56 a écrit:ça donne 2p+1^3+3p+1²+1
il suffit de rajouter le petit +1 àcôté du p
ça prouve pas que ce soit vrai et ça n'empeche pas de mettre des parenthèses kinou

-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Sep 2006, 18:07
par nada-top » 06 Sep 2006, 18:07
(2n+1) = 2n^3 + 3n^2 + n = 6k)
,
dévellope mantenant
(n+2)(2n+3)= ....)
tu dois prouver qu'il s'exprime sous la forme de 6k' tel que

-
kinou56
- Membre Naturel
- Messages: 62
- Enregistré le: 05 Sep 2006, 20:28
-
 par kinou56 » 06 Sep 2006, 18:15
par kinou56 » 06 Sep 2006, 18:15
d'où viens ce k ?
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 06 Sep 2006, 18:18
par BancH » 06 Sep 2006, 18:18
Sans utiliser la récurrence:
Si

et si

alors
(2n+1)\equiv 0[6])
et si

alors

et
(2n+1)\equiv 0[6])
Si

alors
\equiv 0[6])
Si
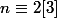
alors

puis si

alors
(2n+1)\equiv 0[6])
et si

alors

et donc
(2n+1)\equiv 0[6])
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Sep 2006, 18:19
par nada-top » 06 Sep 2006, 18:19
d'où viens ce k ?
tu as supposé que
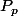
est vraie donc
(2n+1)}{6} \in N)
donc 6 divise
(2n+1))
c-a-d il existe un
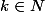
tel que
(2n+1) = 6k)
ok?
-
kinou56
- Membre Naturel
- Messages: 62
- Enregistré le: 05 Sep 2006, 20:28
-
 par kinou56 » 06 Sep 2006, 18:21
par kinou56 » 06 Sep 2006, 18:21
désolé BancH mais je en comprends pas
-
kinou56
- Membre Naturel
- Messages: 62
- Enregistré le: 05 Sep 2006, 20:28
-
 par kinou56 » 06 Sep 2006, 18:22
par kinou56 » 06 Sep 2006, 18:22
oui ça devrait aller
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 06 Sep 2006, 18:23
par BancH » 06 Sep 2006, 18:23
Pas de problème, tu es obligé d'utiliser la récurrence.
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 06 Sep 2006, 18:24
par BancH » 06 Sep 2006, 18:24
kinou56 a écrit:désolé BancH mais je en comprends pas
Pas de problème, tu es obligé d'utiliser la récurrence.
c'était juste pour info ma méthode.
-
kinou56
- Membre Naturel
- Messages: 62
- Enregistré le: 05 Sep 2006, 20:28
-
 par kinou56 » 06 Sep 2006, 18:27
par kinou56 » 06 Sep 2006, 18:27
nada-top: en dévelloppant (n+1)(n+2)(2n+3), je trouve 2n^3+9n²+13n+6.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Sep 2006, 18:27
par nada-top » 06 Sep 2006, 18:27
hérédité : supposons que
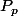
est vraie et démontrons que

est vraie .
alors pour démontrer que

est vrai il faut démontrer que
(n+2)(2n+3)}{6} \in N)
i.e li faut prouver qu'il existe un

tel que
(n+2)(2n+3)=6k')
maintenant dévellope (n+1)(n+2)(2n+3) ...
-
kinou56
- Membre Naturel
- Messages: 62
- Enregistré le: 05 Sep 2006, 20:28
-
 par kinou56 » 06 Sep 2006, 18:28
par kinou56 » 06 Sep 2006, 18:28
j'ai une dernière question sans doute bête mais bon. Comment vous trouvez (n+1)(n+2)(2n+3)?
merci
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Sep 2006, 18:29
par nada-top » 06 Sep 2006, 18:29
nada-top: en dévelloppant (n+1)(n+2)(2n+3), je trouve 2n^3+9n²+13n+6.
oui c bien ça donc maintenant essaye de l'écrire sous la forme 6k'
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Sep 2006, 18:30
par nada-top » 06 Sep 2006, 18:30
j'ai une dernière question sans doute bête mais bon. Comment vous trouvez (n+1)(n+2)(2n+3)?
c
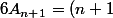 ((n+1)+1)(2(n+1) +1)= (n+1)(n+2)(2n+3))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
