Quadrilatère non croisé.
19 messages
- Page 1 sur 1
Quadrilatère non croisé.
Bonsoir,
je suis sur une leçon de 5ème traitant des vecteurs et des parallélogrammes. On y rencontre souvent la clause "quadrilatère non croisé". Quelle est la (les) méthode(s) pour démontrer qu'un quadrilatère est non croisé ?
En pratique, vérifier qu'il délimite un ensemble du plan convexe ?
Merci pour vos éclaircissements.
je suis sur une leçon de 5ème traitant des vecteurs et des parallélogrammes. On y rencontre souvent la clause "quadrilatère non croisé". Quelle est la (les) méthode(s) pour démontrer qu'un quadrilatère est non croisé ?
En pratique, vérifier qu'il délimite un ensemble du plan convexe ?
Merci pour vos éclaircissements.
Re: Quadrilatère non croisé.
Bonjour Mathelot,
aucun exercice de collège ne demande de démontrer qu'un quadrilatère est non croisé.
On a besoin de cette hypothèse pour utiliser la propriété :
"Si un quadrilatère non croisé a deux côtés opposés de même longueur alors c'est un parallélogramme".
En Seconde, on évite ce problème en la remplaçant par :
"Si deux vecteurs AB et CD sont égaux alors ABDC est un parallélogramme".
(Et réciproquement).
Cordialement,
--
Mateo.
aucun exercice de collège ne demande de démontrer qu'un quadrilatère est non croisé.
On a besoin de cette hypothèse pour utiliser la propriété :
"Si un quadrilatère non croisé a deux côtés opposés de même longueur alors c'est un parallélogramme".
En Seconde, on évite ce problème en la remplaçant par :
"Si deux vecteurs AB et CD sont égaux alors ABDC est un parallélogramme".
(Et réciproquement).
Cordialement,
--
Mateo.
Re: Quadrilatère non croisé.
Salut,
En 5ème, on ne doit pas démontrer qu'un quadrilatère est non croisé, on se contente d'en donner une définition accessible à ce niveau, comme par exemple :
"Un quadrilatère non croisé est un quadrilatère dont un côté ne croise aucun autre côté.", ou quelque chose de similaire et on accompagne de dessins pour aider à comprendre.
Il me semble que ce n'est pas suffisant que pour affirmer que "Si un quadrilatère non croisé a deux côtés opposés de même longueur alors c'est un parallélogramme".
... Ce n'est vrai, me semble-t-il, que si le quadrilatère est plan.
On n'a pas ce soucis, je pense, avec la propriété écrite ainsi : "Si deux vecteurs AB et DC sont égaux alors le quadrilatère ABDC est un parallélogramme".
En 5ème, je présume qu'on ne fait que de la "géométrie plane" et donc que ," il va sans dire" qu'un quadrilatère mentionné dans un exercice est plan, le hic est que par la suite (après la 5ème) les définitions ou propriétés tronquées enseignées restent dans les mémoires et ne sont que trop rarement remises à jour.
Mais, ce n'est que mon avis.

En 5ème, on ne doit pas démontrer qu'un quadrilatère est non croisé, on se contente d'en donner une définition accessible à ce niveau, comme par exemple :
"Un quadrilatère non croisé est un quadrilatère dont un côté ne croise aucun autre côté.", ou quelque chose de similaire et on accompagne de dessins pour aider à comprendre.
Il me semble que ce n'est pas suffisant que pour affirmer que "Si un quadrilatère non croisé a deux côtés opposés de même longueur alors c'est un parallélogramme".
... Ce n'est vrai, me semble-t-il, que si le quadrilatère est plan.
On n'a pas ce soucis, je pense, avec la propriété écrite ainsi : "Si deux vecteurs AB et DC sont égaux alors le quadrilatère ABDC est un parallélogramme".
En 5ème, je présume qu'on ne fait que de la "géométrie plane" et donc que ," il va sans dire" qu'un quadrilatère mentionné dans un exercice est plan, le hic est que par la suite (après la 5ème) les définitions ou propriétés tronquées enseignées restent dans les mémoires et ne sont que trop rarement remises à jour.
Mais, ce n'est que mon avis.
Re: Quadrilatère non croisé.
excusez moi, je me suis trompé, c'est un cours en classe de Seconde.

la propriété est:
"si un quadrilatère non croisé a deux côtés opposés parallèles et de même longueur, alors c'est un parallèlogramme."
la propriété est:
"si un quadrilatère non croisé a deux côtés opposés parallèles et de même longueur, alors c'est un parallèlogramme."
Re: Quadrilatère non croisé.
Bonjour,
mathelot : je crois me souvenir que le sujet était déjà passé sur le forum et que Robot notamment avait donné sa vision relative au quadrilatère non croisé.
peut-être que Ben314 donnera un avis éclairé sur le sujet
mathelot : je crois me souvenir que le sujet était déjà passé sur le forum et que Robot notamment avait donné sa vision relative au quadrilatère non croisé.
peut-être que Ben314 donnera un avis éclairé sur le sujet
Re: Quadrilatère non croisé.
Voir ici. Mathelot s'était déjà posé la question.
Que pensez vous de la condition : pour au moins une des droites passant par deux sommets opposés (une diagonale), les deux autres sommets sont de part et d'autre.
PS. Est-ce qu'en classe de seconde on sait, étant donnés l'équation d'une droite et les coordonnées de deux points, vérifier par le calcul si ces points sont du même côté de la droite ? (Rentrer les points dans l'équation de la droite et vérifier si on obtient le même signe).
PPS. Avec quatre points dont trois ne sont jamais alignés, on peut former trois quadrilatères. Dessinons un (vrai) triangle ABC dans le plan et prolongeons les côtés. On a partagé le plan en 7 régions. Plaçons un point D dans une de ces régions. Suivant la région, les trois quadrilatères formés avec A,B,C,D sont
- soit un convexe et deux croisés,
- soit tous les trois non convexes non croisés.
Je vous laisse voir quelles régions correspondent à quoi.
Que pensez vous de la condition : pour au moins une des droites passant par deux sommets opposés (une diagonale), les deux autres sommets sont de part et d'autre.
PS. Est-ce qu'en classe de seconde on sait, étant donnés l'équation d'une droite et les coordonnées de deux points, vérifier par le calcul si ces points sont du même côté de la droite ? (Rentrer les points dans l'équation de la droite et vérifier si on obtient le même signe).
PPS. Avec quatre points dont trois ne sont jamais alignés, on peut former trois quadrilatères. Dessinons un (vrai) triangle ABC dans le plan et prolongeons les côtés. On a partagé le plan en 7 régions. Plaçons un point D dans une de ces régions. Suivant la région, les trois quadrilatères formés avec A,B,C,D sont
- soit un convexe et deux croisés,
- soit tous les trois non convexes non croisés.
Je vous laisse voir quelles régions correspondent à quoi.
Re: Quadrilatère non croisé.
Quittons maintenant le lycée pour l'université.
Étant donnés trois points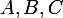 dans le plan muni d'un repère, On définit
dans le plan muni d'un repère, On définit
= \begin{vmatrix} x_A&x_B&x_C\\ y_A&y_B&y_C\\ 1&1&1\end{vmatrix})
Si on se donne quatre points du plan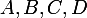 tels qu'il n'y en ait pas trois d'alignés, il y a trois possibilités pour les signes de
tels qu'il n'y en ait pas trois d'alignés, il y a trois possibilités pour les signes de , \Phi(B,C,D), \Phi(C,D,A), \Phi(D,A,B)) :
:
1) tous les quatre de même signe,
2) un d'un signe et trois de l'autre,
3) deux d'un signe et deux de l'autre.
Les situations 1,2,3 dépendent de l'ordre dans lequel on prend les quatre points, mais pas du choix du repère du plan.
Que veulent dire ces trois situations pour le quadrilatère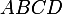 ?
?
Étant donnés trois points
Si on se donne quatre points du plan
1) tous les quatre de même signe,
2) un d'un signe et trois de l'autre,
3) deux d'un signe et deux de l'autre.
Les situations 1,2,3 dépendent de l'ordre dans lequel on prend les quatre points, mais pas du choix du repère du plan.
Que veulent dire ces trois situations pour le quadrilatère
Re: Quadrilatère non croisé.
mathelot a écrit:Bonsoir,
je suis sur une leçon de 5ème traitant des vecteurs et des parallélogrammes. On y rencontre souvent la clause "quadrilatère non croisé". Quelle est la (les) méthode(s) pour démontrer qu'un quadrilatère est non croisé ?
En pratique, vérifier qu'il délimite un ensemble du plan convexe ?
Merci pour vos éclaircissements.
Une façon peut-être tordue: un quadrilatère est croisé si ses cotés ne coincident pas avec l'enveloppe convexe de ses quatre sommets ?
Et pour calculer cette enveloppe convexe, on peut faire appel à la marche de Jarvis
https://fr.wikipedia.org/wiki/Marche_de_Jarvis
Mais pas sur que ce soit très instructif :p
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Quadrilatère non croisé.
Une façon peut-être tordue: un quadrilatère est croisé si ses cotés ne coincident pas avec l'enveloppe convexe de ses quatre sommets ?
Non, cette affirmation est fausse.
Re: Quadrilatère non croisé.
Possibilité :
Si le quadrilatère plan (ABCD) est connu par les coordonnées de ses sommets dans un repère donné, on peut chercher:
- si le point de rencontre des droites (AD) et (BC) est sur le segment [BC]
- si le point de rencontre des droites (AB) et (CD) est sur le segment [AB]
Si une des 2 conditions ci-dessus est réalisée, le quadrilatère ABCD est croisé.
Si aucune des 2 conditions ci-dessus n'est réalisée, le quadrilatère ABCD n'est pas croisé.
Exemple numérique :
Soit A(0 ; 0) ; B(3 ; 0) ; C(-1 ; 1) et D(4 ; 2)
a)
Eq de (AB) : y = 0
Eq de (CD) : y = 0,2.x + 1,2
Le point de rencontre R1 de (AB) et (CD) est R1(-6 ; 0)
Les abscisses de [AB] sont dans [0 ; 3] et donc R1 n'est pas sur [AB]
b)
Eq de (BC) : y = -0,25x + 0,75
Eq de (AD) : y = 0,5.x
Le point de rencontre R2 de (BC) et (AD) est R2(1 ; 1/2)
Les abscisses de [BC] sont dans [-1 ; 3] et donc R2 est sur [BC]
Le quadrilatère ABCD est donc croisé.
Rien vérifié.

Si le quadrilatère plan (ABCD) est connu par les coordonnées de ses sommets dans un repère donné, on peut chercher:
- si le point de rencontre des droites (AD) et (BC) est sur le segment [BC]
- si le point de rencontre des droites (AB) et (CD) est sur le segment [AB]
Si une des 2 conditions ci-dessus est réalisée, le quadrilatère ABCD est croisé.
Si aucune des 2 conditions ci-dessus n'est réalisée, le quadrilatère ABCD n'est pas croisé.
Exemple numérique :
Soit A(0 ; 0) ; B(3 ; 0) ; C(-1 ; 1) et D(4 ; 2)
a)
Eq de (AB) : y = 0
Eq de (CD) : y = 0,2.x + 1,2
Le point de rencontre R1 de (AB) et (CD) est R1(-6 ; 0)
Les abscisses de [AB] sont dans [0 ; 3] et donc R1 n'est pas sur [AB]
b)
Eq de (BC) : y = -0,25x + 0,75
Eq de (AD) : y = 0,5.x
Le point de rencontre R2 de (BC) et (AD) est R2(1 ; 1/2)
Les abscisses de [BC] sont dans [-1 ; 3] et donc R2 est sur [BC]
Le quadrilatère ABCD est donc croisé.
Rien vérifié.
Re: Quadrilatère non croisé.
Comme je l'ai expliqué plus, haut, il est inutile de calculer des points de rencontre de droites.
La diagonale (AC) de l'exemple de Black Jack a pour équation x+y=0. Si on rentre les coordonnées de B et D dans cette équation, on trouve deux valeurs positives : B et D sont du même côté.
La diagonale (BD) a pour équation y-2x+6=0. Si on rentre les coordonnées de A et C dans cette équation, on trouve deux valeurs positives : A et C sont du même côté.
Morale : ABCD est croisé, et on l'a vérifié en calculant seulement deux équations de droites et en rentrant à chaque fois les coordonnées de deux points dans ces équations.
Ça me semble nettement plus économique que de faire deux fois la procédure suivante : calculer deux équations de droites, calculer leur intersection, vérifier si cette intersection appartient à deux segments de ces droites.
La diagonale (AC) de l'exemple de Black Jack a pour équation x+y=0. Si on rentre les coordonnées de B et D dans cette équation, on trouve deux valeurs positives : B et D sont du même côté.
La diagonale (BD) a pour équation y-2x+6=0. Si on rentre les coordonnées de A et C dans cette équation, on trouve deux valeurs positives : A et C sont du même côté.
Morale : ABCD est croisé, et on l'a vérifié en calculant seulement deux équations de droites et en rentrant à chaque fois les coordonnées de deux points dans ces équations.
Ça me semble nettement plus économique que de faire deux fois la procédure suivante : calculer deux équations de droites, calculer leur intersection, vérifier si cette intersection appartient à deux segments de ces droites.
Re: Quadrilatère non croisé.
Chacun sa tactique, ma méthode me semble bien plus compréhensible pour la plupart des élèves du secondaire.
Je vote pour moi.

Je vote pour moi.
Re: Quadrilatère non croisé.
Je m'aperçois que Black Jack ne vérifie que l'appartenance à un seul segment :
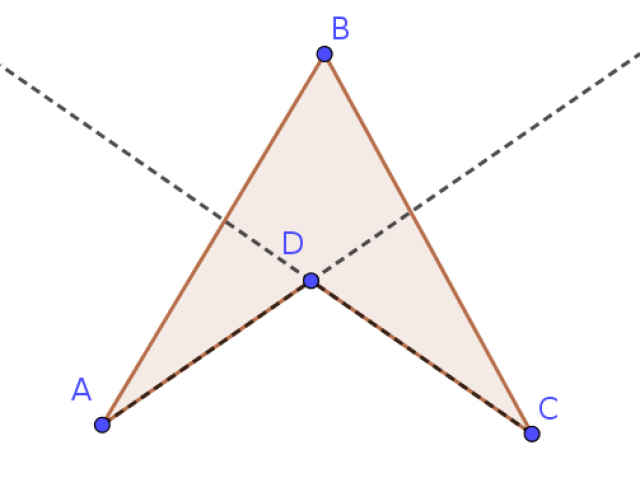
L'exemple suivant montre un cas où les deux conditions sont réalisées et le quadrilatére n'est pas croisé :
Faut-il comprendre le "Si une" de Black Jack comme "Si exactement une" ?
C'est à éclaircir, mais ça ne change de toutes façons pas le fait que sa méthode demande le calcul de quatre équations de droites et de deux intersections de droites.
- si le point de rencontre des droites (AD) et (BC) est sur le segment [BC]
- si le point de rencontre des droites (AB) et (CD) est sur le segment [AB]
Si une des 2 conditions ci-dessus est réalisée, le quadrilatère ABCD est croisé.
L'exemple suivant montre un cas où les deux conditions sont réalisées et le quadrilatére n'est pas croisé :

Faut-il comprendre le "Si une" de Black Jack comme "Si exactement une" ?
C'est à éclaircir, mais ça ne change de toutes façons pas le fait que sa méthode demande le calcul de quatre équations de droites et de deux intersections de droites.
Re: Quadrilatère non croisé.
GaBuZoMeu a écrit:Une façon peut-être tordue: un quadrilatère est croisé si ses cotés ne coincident pas avec l'enveloppe convexe de ses quatre sommets ?
Non, cette affirmation est fausse.
Salut Gabuzomeu,
Pourrais-tu m'expliquer un peu s'il te plait ?
J'ai pas la bonne vision de ce qu'est un quadrilatère croisé?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Quadrilatère non croisé.
Définition : un quadrilatère croisé est un quadrilatère qui a deux côtés opposés qui se coupent. C'est la définition qu'on trouve partout.
Le quadrilatère dessiné ci-dessus n'est pas croisé. C'est un quadrilatère non croisé et non convexe. Ses côtés ne coïncident pas avec les côtés de l'enveloppe convexe des quatre sommets du quadrilatère.
PS. Dans une page web intitulée "Les quadrilatères au collège", j'ai trouvé :
Mais, selon Black Jack, la méthode qui en découle pour vérifier si un quadrilatère est croisé est bien moins compréhensible pour la plupart des élèves du secondaire. Ni Black Jack ni moi ne sommes enseignants du secondaire. Qu'en pensent ces derniers ?
Le quadrilatère dessiné ci-dessus n'est pas croisé. C'est un quadrilatère non croisé et non convexe. Ses côtés ne coïncident pas avec les côtés de l'enveloppe convexe des quatre sommets du quadrilatère.
PS. Dans une page web intitulée "Les quadrilatères au collège", j'ai trouvé :
Un quadrilatère est croisé si pour chaque diagonale, les deux autres sommets sont dans un même demi-plan par rapport à cette diagonale ;
Mais, selon Black Jack, la méthode qui en découle pour vérifier si un quadrilatère est croisé est bien moins compréhensible pour la plupart des élèves du secondaire. Ni Black Jack ni moi ne sommes enseignants du secondaire. Qu'en pensent ces derniers ?
Re: Quadrilatère non croisé.
Suite à une bonne remarque, je corrige :
Si le quadrilatère plan (ABCD) est connu par les coordonnées de ses sommets dans un repère donné,
- si le point de rencontre des droites (AD) et (BC) est sur le segment [AD] ET sur le segment [BC]
OU
- si le point de rencontre des droites (AB) et (CD) est sur le segment [AB] ET sur le segment [CD]
... le quadrilatère ABCD est croisé.
Sauf nouvelle étourderie

Si le quadrilatère plan (ABCD) est connu par les coordonnées de ses sommets dans un repère donné,
- si le point de rencontre des droites (AD) et (BC) est sur le segment [AD] ET sur le segment [BC]
OU
- si le point de rencontre des droites (AB) et (CD) est sur le segment [AB] ET sur le segment [CD]
... le quadrilatère ABCD est croisé.
Sauf nouvelle étourderie
Re: Quadrilatère non croisé.
Je m'étonne du silence de mathelot. C'est pourtant lui qui a initié ce fil sur les quadrilatères croisés ou non croisés ...
Re: Quadrilatère non croisé.
je m'instruis. je lis le thread avec attention.
il est possible que ni ABCD ni ABDC ne soient croisés (dans le cas où ABCD n'est pas convexe)
il est possible que ni ABCD ni ABDC ne soient croisés (dans le cas où ABCD n'est pas convexe)
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
