Ptite equation a resoudre ds C

par **mostdu95** » 27 Sep 2007, 19:04

bonsoir:
resoudre danc C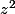

2iz

1+2i = 0
bon j'ai calculer delta et je trouve 16+8i et je me bloque ladessus je n'est jamais fait d'equation ou je trouve un delta imaginaire
aider moi et merci d'avance

par **Imod** » 27 Sep 2007, 19:24

Tu es sûr de ton delta ?

Imod

par **mostdu95** » 27 Sep 2007, 19:29

[quote="Imod"]Tu es sûr de ton delta ?

Imod[/QUOTE+Imod]
oui en effet j'ai fait delta=(-2i)²-4(-1+2i)=-4+4-8i=-8i ok mais c pareil je trouve un delta imaginaire je sais pô comment extraire les racines

par **mostdu95** » 27 Sep 2007, 19:29

Imod a écrit:Tu es sûr de ton delta ?

Imod

oui en effet j'ai fait delta=(-2i)²-4(-1+2i)=-4+4-8i=-8i ok mais c pareil je trouve un delta imaginaire je sais pô comment extraire les racines
aide moi s'il te plait

par **Imod** » 27 Sep 2007, 19:37

As-tu essayé 2-2i ?

Imod

par **mostdu95** » 27 Sep 2007, 19:39

Imod a écrit:As-tu essayé 2-2i ?

Imod

comment ça ? il faut cherché une solution evidente ??
et pourquoi o peut pas la resoudre avec delta ??

par **Imod** » 27 Sep 2007, 19:43

Calcule

et reviens après :we:

Imod

par **emdro** » 27 Sep 2007, 19:46

Bonjour,

les équations du second degré sont au programme si elle sont à coefficient réel.
Au lycée, il n'est pas question de calculer le discriminant avec des coefficients complexes.

Ici, on a une racine évidente: 1
Factorise par (z-1)

par **mostdu95** » 27 Sep 2007, 19:48

je trouve -8i i.e mon delta
on conclut comment apres ?? y'a t-il unbe methode a suivre lorsqu'on trouve delta imaginaire par ce que ds mon cas je trouve un delta plus simple mais imaginons delta= 12+19i on fait comment

par **Imod** » 27 Sep 2007, 19:52

Suis les conseils d'Emdro ( les indications que je t'ai donné ne peuvent sûrement pas t'aider ) :we:

Imod

par **mostdu95** » 27 Sep 2007, 19:55

en fait ce que je veux c'est plutot une methode géneral pour resoudre ce genre d'equation

par **Imod** » 27 Sep 2007, 19:59

La méthode , tu l'as , mais c'est pas toujours facile !!!!

Imod

par **emdro** » 27 Sep 2007, 20:02

Tu apprendras plus tard, cette année, à calculer les deux racines carrées d'un nombre complexe. Tu pourras alors [hors du cadre du programme] utiliser la méthode du discriminant (qui bloque au moment où on doit calculer "racine de Delta").

Pour l'instant, si tu as des coefficients non réels, c'est que tu as des solutions évidentes, et donc tu peux factoriser. C'est cela la méthode.

par **lapras** » 27 Sep 2007, 20:06

Bonsoir,
emdro,
qu'entends tu par "calculer les deux racines carrées d'un nombre complexe" ?

par **mostdu95** » 27 Sep 2007, 20:10

La méthode , tu l'as , mais c'est pas toujours facile !!!!
d'accord donc des que je trouve un delta imaginaire je cherche une solution de delta comme ce que tu m'avait proposé

apres on trouve comment les solutions finales ?

par **emdro** » 27 Sep 2007, 20:11

Pour tout a complexe, il existe deux solutions à l'équation z²=a (elles sont confondues si et seulement si a=0). Ces deux solutions sont appelées racines carrées de a.
Si a est un réel positif, il s'agit de

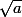
et

.
De manière générale, on les cherche avec module et argument.

par **emdro** » 27 Sep 2007, 20:13

mostdu95 a écrit:d'accord donc des que je trouve un delta imaginaire je cherche une solution de delta comme ce que tu m'avait proposé apres on trouve comment les solutions finales ??

Si tu notes

une racine de

, les deux racines sont

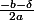
et

.
Cela ne te surprendra pas...

par **emdro** » 27 Sep 2007, 20:16

mostdu95 a écrit:La méthode , tu l'as , mais c'est pas toujours facile !!!!

Si tu es en TS, c'est toujours facile. :happy2:

par **mostdu95** » 27 Sep 2007, 20:23

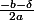
emdro a écrit:Si tu notes une racine de , les deux racines sont et .
Cela ne te surprendra pas...

ok c'est bon je trouve 1 et 2i-1
yes merci beaucoup

par **emdro** » 27 Sep 2007, 20:25

Cela marche, mais fais attention: tu as le choix entre:
* une méthode simple au programme (factoriser par z-1)
* une grosse méthode générale (compliquée) hors programme

Pour éviter le ridicule, fais le bon choix! :id:

Ptite equation a resoudre ds C

ptite equation a resoudre ds C

Qui est en ligne