Ptite quest° CONGRUENCE....URGENT!!!!!

par **izamane95** » 21 Nov 2006, 19:25

:help:
bonsoir voilà l'ennoncé:
determiner l'enssemble

des entiers relatifs x tels que le nombre n = x²+x-2 est divisible par 7 :hein: :hein:
aidez moi

par **Sapphire** » 21 Nov 2006, 19:26

Tu cherches donc les nombres n tels que x² + x - 2 "congru à" 0 (mod. 7) ...

Tu y vois plus clair ?

par **izamane95** » 21 Nov 2006, 19:31

en fait ça je l'ai ecris ds mon brouill ms je vois vraiment rien
en fait je pense a dire
x² = 0(7) et (x-2)=0(7) :hein: j'ai tors????

par **Sapphire** » 21 Nov 2006, 19:33

Euh ... !

Comment tu peux conclure ça ??!! :doh:

par **izamane95** » 21 Nov 2006, 19:39

sinon
j'ecris x² - x = -2(7)
x(x+1) = -2(7)
donc soit x=-2(7) alors x+1=1(7) dc x=0(7) (= pour dire congru)
mais là je vais rien trouvé ça m'avance pas

par **izamane95** » 21 Nov 2006, 19:54

ahhhhhhhhhhhhh c bon j'ai trouvé je retire toutes les conneries que j'avais dit :euh:

par **Sapphire** » 21 Nov 2006, 19:55

Attention !
L'énoncé te dit : x² + x - 2 CONGRU A 0 [7]

Pour écarter les x du même côté, il faut ajouter 2 de chaque côté :
On obtient : x² + x CONGRU A +2 (et pas -2) [7] ...

par **izamane95** » 21 Nov 2006, 20:01

oui oui c bon j'ai trouvé . il fallait pas mettre le-2 de l'autre coté ,il faut le laisser comme il est et faire ou dire que x est congru a tout les restes de 7 voir 0,1,2,3,4,5,6, aprés on conclu pour x²+x-2 :king:

par **Sapphire** » 21 Nov 2006, 20:02

C'est une méthode ;)

Tu trouves bien x = 7k + 1 ?

par **izamane95** » 21 Nov 2006, 20:15

pourquoi c'est 7k +1????? EN FAIT j'ai pas encor conclu ou si tu veux j'arrive pas a conclure

alors

et la meme chose pour les autres
ms on fait comment fait-on pour conclure :euh: (c bete comme question je sais ms c la life et les maths... :ptdr: !!!!!)

par **Sapphire** » 21 Nov 2006, 20:22

Je comprends rien la balise a pas marché ^^

Moi je fais : x²+x congru à 2 [7]

donc x(x+1) congru à 2 [7]
x congru à 2 [7] ou x congru à 1 [7].

Mais la première solution ne fonctionne pas jy ai pas encore vraiment réfléchi.

par **izamane95** » 21 Nov 2006, 20:23

ms regarde ce que j'ai ecris là (derriere :page 1)c'est un peu clair !!!

par **Imod** » 21 Nov 2006, 20:25

As-tu essayé de factoriser

?

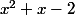
Imod

par **Sapphire** » 21 Nov 2006, 20:25

Mouais je comprends pas trop trop ta méthode ..
Jsuis pas sur de la mienne ;)

Le point d'interrogation représente quoi ? La puissance ?

par **izamane95** » 21 Nov 2006, 20:26

x²+x-2 = (x-1)(x+2)
veut dire

et

haaaaaaa donc

et

c juste ça les solutions???!!!!! :mur:
ms ils demondent de trouver un enssemble de solut°

par **izamane95** » 21 Nov 2006, 20:27

Le point d'interrogation représente quoi ? La puissance ?

c x²( ça le fait pas ds le truc )!!!!!!!!!!!!!!!!!

par **Sapphire** » 21 Nov 2006, 20:31

Voilà.

Tu as trouvé en factorisant !

7 est un nombre premier. Un produit de facteurs est congru à 0 modulo 7 si l'un des facteurs est congru à 0 modulo 7.

Donc x-1 congru à 0 [7] ou x+2 congru à 0 [7]

Tu obtiens : x congru à 1 modulo 7
x congru à -2 modulo 7

D'ou x = 7k + 1 ou x = 7k - 2

D'ou mon résultat de toute à l'heure ;)

par **Sapphire** » 21 Nov 2006, 20:33

Je crois (je ne suis pas sûr) que ce sont les seules solutions.
J'avais pas vu ta modification désolé :++:

par **izamane95** » 21 Nov 2006, 20:36

D'ou x = 7k + 1 ou x = 7k - 2

avec k nn nul et k appartient à N :ruse:

je ne suis pas sûr) que ce sont les seules solutions.

je crois que c'est les seuls solutions

par **izamane95** » 21 Nov 2006, 20:38

un grand merci quand meme a IMODE qui m'a mis ds la bonne piste

Ptite quest° CONGRUENCE....URGENT!!!!!

ptite quest° CONGRUENCE....URGENT!!!!!

Qui est en ligne