Prouver qu'une droite est asymptote à la courbe d'une foncti
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 30 Nov 2006, 20:58
par Baba » 30 Nov 2006, 20:58
Salut à tous !!
Voilà je vous expose mon problème:
Je dois prouver que la droite D d'équation y=2-x est asymptote à la courbe C qui est la courbe représentative de la fonction f(x)=(2-x)(
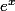
+1)
Pour cela je dois prouver que
(e^{x}+1)-(2-x)]=0})
Mais le seul truc c'est que je sais pas comment faire, j'y arrive pô....
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 30 Nov 2006, 21:07
par Elsa_toup » 30 Nov 2006, 21:07
Bonsoir,
Factorise par (2-x)...
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 30 Nov 2006, 21:19
par Baba » 30 Nov 2006, 21:19
En effet c'est tout simple, je me demande comment j'ai pas vu ça !! :id:
Ca fait
[(e^{x}+1)-1])
Et quand x tend vers - l'infini le 2ème membre tend vers 0, ce qui fait que le tout tend vers 0.
OK merci !
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 30 Nov 2006, 22:22
par prody-G » 30 Nov 2006, 22:22
euh c'est pas la bonne justification :
quand A --> +inf
et B --> 0
A x B ne tend pas vers 0
tu dois passer par une croissance comparée pour justifier le résultat
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 30 Nov 2006, 22:35
par prody-G » 30 Nov 2006, 22:35
tiens prends par exemple la fonction f(x) = (x²+2)/x = (x²+2) x (1/x)
lim x²+2 = +inf
+inf
lim 1/x = 0
+inf
lim f(x) = +inf (et pas 0)
+inf
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
