Programme de Seconde ?

[Lostounet]

Bonjour !

J'aimerais avoir vos conseils/avis/propositions concernant le programme de seconde, qui est facile bien évidemment, mais j'aimerais savoir un peu précisément les notions un peu ambigües/ intéressantes, vu que j'ai envie d'être (très) en avance par rapport aux autres l'année prochaine (et m'ennuyer en cours, par conséquent).

Si vous avez des liens de sites intéressants, merci de me les passer :)
Même ayant déjà fait quelques recherches, je n'ai rien trouvé d'intéressant.. :--:

P.S:
Bene, je ne veux évidemment pas te déranger en ces vacances bien méritées pour toi :triste: C'est pour cela que je fais demande en public :++: :triste:

[Anonyme]

Salut,

En soi, le programme de seconde ne présente aucune difficulté. Il se place dans la continuité de la troisième et si tu as bien suivi dans cette classe, si tu es rigoureux et efficace, il n'y a pas de raison d'éprouver des difficultés.
Le chapitre vraiment "spécial" je dirais, c'est celui de géométrie dans l'espace : le raisonnement n'est pas difficile, mais cela change un peu du reste. J'ai beaucoup apprécié la partie analyse fonctionnelle du programme, rien de très méchant non plus, d'autant plus que le programme subit quelques modifications et que tout devient très calculatoire.
En ce qui concerne les sites intéressants, tu peux te mesurer aux exercices de M. Alarcon, souvent d'un bon (très bon) niveau. Dis-le moi, je te les scanne si tu veux.

[Dinozzo13]

Salut !
Après, ça dépend de ce que tu as vu en 3e, les programmes de amths sont peut-être différent.
PAr exemple, les vecteurs ne sont plus abordés en 3e, on ne les découvre donc qu'en 2nde.
A part ça, pas grand chose de nouveau, à part un peu plus de rigueur :++:

[Lostounet]

Salut,

En soi, le programme de seconde ne présente aucune difficulté. Il se place dans la continuité de la troisième et si tu as bien suivi dans cette classe, si tu es rigoureux et efficace, il n'y a pas de raison d'éprouver des difficultés.
Le chapitre vraiment "spécial" je dirais, c'est celui de géométrie dans l'espace : le raisonnement n'est pas difficile, mais cela change un peu du reste. J'ai beaucoup apprécié la partie analyse fonctionnelle du programme, rien de très méchant non plus, d'autant plus que le programme subit quelques modifications et que tout devient très calculatoire.
En ce qui concerne les sites intéressants, tu peux te mesurer aux exercices de M. Alarcon, souvent d'un bon (très bon) niveau. Dis-le moi, je te les scanne si tu veux.

Merci de ta réponse si rapide

Je vois un peu. Sinon, est-ce que je suis capable de faire ces exercices? Si oui, j'en serais très reconnaissant, d'avoir 1 ou 2 en guise d'exemples

Merci d'avance!

[Lostounet]

Salut !
Après, ça dépend de ce que tu as vu en 3e, les programmes de amths sont peut-être différent.
PAr exemple, les vecteurs ne sont plus abordés en 3e, on ne les découvre donc qu'en 2nde.
A part ça, pas grand chose de nouveau, à part un peu plus de rigueur :++:

Merci pour la réponse!

En effet, les programmes peuvent différer. Par exemple moi j'ai déjà fait un peu de géométrie analytique (équations de droites, vecteurs) et c'était inclu pour mon brevet.

[Dinozzo13]

Ouais donc voilà, maintenant on en a plus en 3e.
Par contre si tu veux, je peux te donner une méthode que j'ai vue en hors programme en classe de seconde pour résoudre des système de deux équations à 2 inconnues voire même de 3 équations à 3 inconnues (C'est une méthode vue en 1re ES, car mon prof de 2nde en avait ^^)
Avantage : Ca marche tout le temps.
Inconvénient : Ne pas se tromper dans l'ordre des calculs et dasn les calculs eux-mêmes.
Ca te dit ?

[Anonyme]

Ok Je te propose deux exercices que propose ce professeur aux élèves de 3e qui arrivent en seconde donc tu n'as rien besoin de plus que ce que tu as appris cette année ! ^^
Exercice 1
Un vendeur doit déterminer le prix optimum d’un article. Il dispose des données suivantes:
si le prix de l’article est de 75 euros, il vendra 100 de ces articles. Chaque fois que le prix de vente est augmenté de 5 euros, 20 articles de moins sont vendus. Chaque fois que le prix de vente est dimininué de 5 euros, 20 articles de plus sont vendus. Le coût de production de cet article est de 30 euros. Quel est le prix de vente optimum (celui qui rend le bénéfice maximum) ?
Exercice 2
Sur une étagère sont rangés 50 livres, certains de mathématiques, les autres de physique. Il n’y a pas
deux livres de physique côte à côte, mais tout livre de mathématiques est à côté d’un autre livre de
mathématiques. Parmi les phrases suivantes, une seule peut être fausse. Indiquer laquelle en le justifiant.
a) Il y a au moins 32 livres de mathématiques.
b) Il y a au plus 17 livres de physique.
c) Il y a trois livres de mathématiques à la suite.
d) S’il y a 17 livres de physique, alors il y a un livre de physique à l’une ou l’autre des extrémités de
l’étagère.
e) Sur 9 livres qui se suivent, il y a au moins 6 livres de mathématiques.

bon courage (C'est pas trop dur ça !)

[Lostounet]

Ouais donc voilà, maintenant on en a plus en 3e. Par contre si tu veux, je peux te donner une méthode que j'ai vue en hors programme en classe de seconde pour résoudre des système de deux équations à 2 inconnues voire même de 3 équations à 3 inconnues (C'est une méthode vue en 1re ES, car mon prof de 2nde en avait ^^) Avantage : Ca marche tout le temps. Inconvénient : Ne pas se tromper dans l'ordre des calculs et dasn les calculs eux-mêmes. Ca te dit ?

Oui !! Cela m'intéresse

J'ai déjà appris les méthodes suivantes 'simples': Combinaison/ Substitution/ Comparaison

Merci

[Dinozzo13]

cool :++:
j'te prépare ça

[Lostounet]

Exercice 1
Un vendeur doit déterminer le prix optimum d’un article. Il dispose des données suivantes:
si le prix de l’article est de 75 euros, il vendra 100 de ces articles. Chaque fois que le prix de vente est augmenté de 5 euros, 20 articles de moins sont vendus. Chaque fois que le prix de vente est dimininué de 5 euros, 20 articles de plus sont vendus. Le coût de production de cet article est de 30 euros. Quel est le prix de vente optimum (celui qui rend le bénéfice maximum) ?

Merci beaucoup Titux

Est-ce le troisième ?
Je montre ma méthode?

[Dinozzo13]

Soit le système suivant :

où et désigne des réels quelconque.

Avant toute chose on calcule ce que l'on appelle le déterminant du système, qui est définit par :

Ensuite, deux cas s'offrent à toi :

1° Si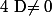 alors le système est dit de Cramer et ne possède donc qu’un seul et unique couple pour solution.
Ainsi, on calcule deux autres déterminants et définis par :
et .
Et donc le couple solution du système est défini par :
.

2° Si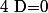 alors le système admet soit une infinité de solutions ou bien aucune.
Par conséquent, il existe donc un réel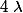 tel que et .
Donc ici, tout ce que tu as à faire, c'est d'exprimer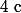 en fonction de .
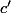- Si alors le système admet une infinité de solutions
- Si alors le système n'admet aucune solutions.

Cette résolution est surtout pratique lorsqu'on a des racines carrées ou des coefficient compliqués en et .

Voilà, désolé pour l'attente ^^

[Lostounet]

Soit le système suivant :

où et désigne des réels quelconque.

Avant toute chose on calcule ce que l'on appelle le déterminant du système, qui est définit par :

Ensuite, deux cas s'offrent à toi :

1° Si alors le système est dit de Cramer et ne possède donc qu’un seul et unique couple pour solution.
Ainsi, on calcule deux autres déterminants et définis par :
et .
Et donc le couple solution du système est défini par :
.

2° Si alors le système admet soit une infinité de solutions ou bien aucune.
Par conséquent, il existe donc un réel tel que et .
Donc ici, tout ce que tu as à faire, c'est d'exprimer en fonction de .
- Si alors le système admet une infinité de solutions
- Si alors le système n'admet aucune solutions.

Cette résolution est surtout pratique lorsqu'on a des racines carrées ou des coefficient compliqués en et .

Voilà, désolé pour l'attente ^^

Merci Dinozzo !
C'est vraiment sympa! (Les Balises ont probablement été pénibles à mettre :triste:)

Puis-je essayer avec un exemple ? (Je le facilite pour voir).

Soit à résoudre:


Calculons le déterminant donné par:





Alors il s'agit d'un système dit de Cramer, et admet donc un couple unique (x ; y) comme solution.

Ainsi, calculons les deux autres déterminants et tels que:


.

Et le couple est (5 ; 3)!

Oui effectivement, c'est plus simple pour les racines carrées et coefficients durs!

Mais ce qui me fascine, et qui me rend :hein: : Comment quelqu'un aurait-il un jour pu concevoir cet outil?

PS: Tu n'as pas à t'excuser, c'est surtout à moi de le faire de t'imposer une tâche supplémentaire ! Merci encore

[benekire2]

Salut !

J'ai pas pu participer à cette session pour le moins ... nocturne !

Lostounet, sache que tu ne vas pas me déranger en m'écrivant et en me demandant comment progresser, je suis toujours très ravi de t'aider (pendant que je peut encore ) :we:

Mon avis c'est que il faut que tu te repose avant d'arriver en seconde, profite des tes vacances, et puis si tu as envie commence le prog. Ou alors deuxième solution ( je sais pas du tout si tu aime) tu t'intéresse aux exos style olympiade. En tout cas ne t'en fais pas. Essaye (si tu peut) de te procurer un livre de seconde du liban, ou alors achète des bouquins parascolaires genre "Prepabac" , et de travailler avec.

Voilà ce que je te conseille !

[Lostounet]

Salut !

J'ai pas pu participer à cette session pour le moins ... nocturne !

Lostounet, sache que tu ne vas pas me déranger en m'écrivant et en me demandant comment progresser, je suis toujours très ravi de t'aider (pendant que je peut encore ) :we:

Mon avis c'est que il faut que tu te repose avant d'arriver en seconde, profite des tes vacances, et puis si tu as envie commence le prog. Ou alors deuxième solution ( je sais pas du tout si tu aime) tu t'intéresse aux exos style olympiade. En tout cas ne t'en fais pas. Essaye (si tu peut) de te procurer un livre de seconde du liban, ou alors achète des bouquins parascolaires genre "Prepabac" , et de travailler avec.

Voilà ce que je te conseille !

:ptdr: Merci :id:

Je vais bien profiter de mes vacances, bien entendu, mais j'aimerais juste jeter un coup d'œil pour éviter les mauvaises surprises ..!

Les Olympiades ? N'est-ce pas encore un peu tôt pour moi? Je peux essayer. Je vais acheter le livre de seconde du Liban, mais ce sera dur pour moi de faire les exos seul :S La Géométrie était quasi-pas faisable en 3e déjà, dans l'ensemble.

Je vais voir du côté prépabac alors.

Tes Réponses sont toujours très utiles Merci encore!

[Dinozzo13]

Tiens je te donne un autre exo.

Soit le système suivant :

où m désigne un paramètre réel.
Résoudre, suivant les valeurs du réel , le système.

[Dinozzo13]

Pour ton plus grand plaisir :ptdr: je te concocte un petit exo pour résoudre un système de 3 équations à trois inconnues :++:

[Lostounet]

Merci! Je vais essayer. ;)

[Lostounet]

Tiens je te donne un autre exo.

Soit le système suivant :

où m désigne un paramètre réel.
Résoudre, suivant les valeurs du réel , le système.

Cherchons le déterminant du système:






x =
x =


De même pour y:

y =


Donc euh, on va dire que:

Et


Est-ce cela?
Qu'est-ce qu'un paramètre / Déterminant? Désolé, tout cela est nouveau pour moi :triste:
Merci de m'éclaircir.
Et vraiment désolé pour l'attente :hum: :triste:

[Olympus]

La technique présentée par Dinozzo est dans notre programme marocain de Seconde, donc c'est pas du hors-programme chez nous ...

@Lostounet : la seconde n'est vraiment pas à prendre au sérieux, les seules nouveautés que tu y verras sont le taux de variation d'une fonction ( que tu oublieras très vite plus tard une fois la dériviation faite en Première ), gros focus sur l'étude des signes, la méthode du discriminant et factorisation des polynômes à partir de racines évidentes . Pour la géométrie dans l'espace, euh je ne sais pas, mais osef, tu vas la refaire en Première avec des outils analytiques . Vu la facilité du programme de Seconde, tu peux te permettre de travailler un peu moins d'exos en Maths pour te concentrer sur d'autres matières .

[Dinozzo13]

on appelle paramètre une sorte de demie inconnue : c'est une inconnue mais pas à prendre comme s'il s'agissait d'une inconnue comme x ou y.
Il faut le considérer comme un valeur fixe.
Donc en calculant tu dois déjà regarder s'il existe des valeurs de m qui rendent nulles D. Puis tu fait de même pour toutes les valeurs de m différentes de celles qui rendent D nul.