Programme de Seconde ?

[Lostounet]

Tiens je te donne un exercice qui traite du nombre d'or, sujet souvent abordé en 2nde voire même en 3e, qui est toujours bon de savoir faire.
Celui-ci à été tiré d'un devoir de 2nde de mon frère cette année, amuse-toi bien :++:

Le réel est appelé nombre d'or. est une lettre grec nommée "phi".
1°) Calculer puis sans radical au dénominateur.
2°) En déduire que :
3°) En déduire en fonction de sous la forme , où et sont deux entiers à déterminer.


4°) En déduire et en fonction de .
Donner l'expression numérique de .
5°) En déduire celle de .

Salut Dino! Merci pour l'exo

1°) =
=
=

=
=
=
=
=
=
=

Tout bon, je continue?

2)
On en déduit que:
=

Alors:





3) (Fait, une minute).

[Lostounet]

:ptdr: Non, je n'ai toujours pas officiellement réussi, et faudra attendre mi-juillet pour voir si j'ai réussi!!! Mais je suis très optimiste :zen:

L'épreuve de maths a été excessivement longue!!! L'exo de géométrie m'a pris environ 1 heure, et celui de géométrie analytique m'a pris aux alentours des 30 minutes, ne me laissant que 30 minutes pour tout ce qui est calcul/factorisations/statistiques/inéquations..!
Mais au final, je m'en suis sorti :D

Faut dire qu'une quasi majorité n'a pas pu terminer :S

[Dinozzo13]

oui c'est bon :++:
ce n'est que du calcul ^^

[Lostounet]

Dino, j'ai trouvé: :hum:

[Olympus]

Plutôt .

[Nightmare]

Si le programme de seconde ne présente pas de réelles difficultés dans les notions enseignées, c'est quand même un programme difficile dans le sens ou on commence à apprendre aux élèves à être rigoureux, méthodiques, logiques... bref, tout ce qui fait les maths en dehors des formules.

Donc la seconde n'est pas une classe que l'on passe les doigts dans le nez, d'ailleurs beaucoup d'élèves échouent à l'entrée du secondaire alors qu'ils n'étaient pas du tout mauvais au collège. Alors même toi, Lostounet qui semble avoir déjà de l'aisance en maths, ne va pas en seconde en te disant que ce sera une année facile en maths, même si ce sera surement le cas, mieux vaut toujours avoir à l'esprit qu'une année scolaire, tant qu'on ne l'aura pas vécu, nous apportera toujours quelque chose qu'on n'aura pas eu avant.

[Lostounet]

Oui, oui exactement! Excusez-moi :O!

Je vois à présent

Si:

[Lostounet]

Si le programme de seconde ne présente pas de réelles difficultés dans les notions enseignées, c'est quand même un programme difficile dans le sens ou on commence à apprendre aux élèves à être rigoureux, méthodiques, logiques... bref, tout ce qui fait les maths en dehors des formules.

Donc la seconde n'est pas une classe que l'on passe les doigts dans le nez, d'ailleurs beaucoup d'élèves échouent à l'entrée du secondaire alors qu'ils n'étaient pas du tout mauvais au collège. Alors même toi, Lostounet qui semble avoir déjà de l'aisance en maths, ne va pas en seconde en te disant que ce sera une année facile en maths, même si ce sera surement le cas, mieux vaut toujours avoir à l'esprit qu'une année scolaire, tant qu'on ne l'aura pas vécu, nous apportera toujours quelque chose qu'on n'aura pas eu avant.

Évidemment, mais il ne faut pas non plus paniquer (comme je fais en général)..! C'est pour cela que j'essaye de prendre de l'avance en demandant conseil

[Olympus]

Autre méthode :





PS : une des trucs à ne pas oublier en Seconde c'est de savoir quand tes équivalences s'arrêtent et deviennent des implications, ici c'est bon car est positif . Peut-être qu'un petit cours de logique t'intéresserait ( bien qu'hors programme, cela t'aiderait à mieux rédiger des démos ) ?

[Lostounet]

Oui Olympus j'aimerais bien avoir une idée :D

Et pour le quatre Dino, le premier, c'est la même technique (que j'ai fait)?
Je continue.

[Dinozzo13]

C'est ça.
Par contre le calcul de n'est pas fini.

[benekire2]

Salut ! Le nombre d'or .. c'est marrant ..

On a de manière générale.
De plus tu pourra t'amuser a démontrer que

et il est même facile de montrer que avec F la suite de fibonacci on a :



Et il y en a un paquet d'autres ... :zen:

[Olympus]

Voici quelques notions :

Proposition : un truc qui a un sens, cela peut-être un énoncé mathématique ( "Le carré d'un réel est toujours positif" ), mais aussi quelque chose du genre "Dieu existe" etc...

Porte logique : vulgairement, c'est comme des opérateurs algébriques (+, /, -, * ... ) mais dans la logique, en gros, t'as les trois portes logiques élémentaires suivantes : NON ( ), OU ( ) , ET ( ) .

La proposition "NON p" est vraie si et seulement si p est fausse . En d'autres mots, la porte NON "inverse" la valeur de vérité de "p" ( si p est fausse, alors NON p est vraie, si p est vraie, alors NON p est fausse ) .

La proposition "p OU q" ( avec p et q deux propositions ) est vraie si et seulement si une des deux propositions est vraie, ou les deux à la fois .

La proposition "p ET q" est vraie si et seulement si les deux propositions sont toutes les deux vraies .

Loi de Morgan :

.

Implication :

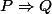
Si t'as dans un exo "Montrer que si P alors Q", alors cela équivaut à montrer que , et c'est ce qu'on appelle une implication .

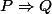
L'implication est définie par : .

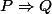
Donc d'après cette définition, est vraie si et seulement si : P et Q sont vraies à la fois, ou P fausse et osef de Q ( "Du vrai suit le vrai... Du faux suit le faux... Du faux suit le vrai... Mais du vrai, le faux ne peut s'ensuivre" ) .

Implications successives :

T'as toujours l'implication suivante :



( il suffit de raisonner par récurrence )

Montrer qu'une implication est vraie :

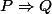
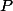
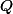
Donc, on voit que pour montrer que l'implication est vraie, il suffit de supposer que est vraie, et aller par implications jusqu'à ce qu'on trouve que est vraie aussi .

Méthode alternative, la contraposée :

Sans ressortir le bagage logique pour prouver que la contraposée a la même valeur de vérité que l'implication, il suffit de te dire que si P implique Q, alors cela voudrait dire que si Q est fausse, c'est que bien évidemment P est fausse .

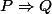
Donc pour montrer que , il suffit de montrer que .

Un exemple tiré de Wikipédia serait : "S'il pleut, alors le sol est mouillé" . Sa contraposée est "Si le sol n'est pas mouillé, alors il ne pleut pas" . Il est tout à fait clair que les deux propositions sont équivalentes .

[benekire2]

après je pense que pour un term c'est bien d'avoir des notions de logique, mais pour un élève de seconde... je sais pas. ( Mais ça ne peut pas faire de mal ... ) :we:

[Olympus]

Pour un 2nde, cela lui éviterait des erreurs trop souvent causées par une mauvaise gestion des implications/équivalences ^^

[benekire2]

Oui, je sais que c'est ce que tu voulais faire, mais là c'est "la théorie" et la pratique c'est que en lisant cela il n'est pas plus avancé pour trouver où est l'erreur là dedans :

|x| -1 -1-x -1-x -1 (x-1)(x²+x+1)=0 x^3=1 x=1

Et bien, sûr vu que tu as donné la définition de l'équivalence, alors il est évident que la phrase ( 2=1 => x^n=0 pour x différent de 0 ) ou tout autre chose. D'où l'importance de remarque que si (P=>Q) est vraie, alors si P aussi l'est on a Q vérifiée.

Et a ce titre , petit exercice : Montrer que pour tout x de [0,1]

A montrer proprement. Les lycéens peuvent jouer ( Jusqu'en Term, si si)

[Olympus]

Je terminerai un autre jour sur les équivalences, car demain je passe l'examen régional d'histoire/géo ( j'ai passé celui de Français/Instruction islamique/Arabe hier, bien pour le français, moyen pour l'instruction islamique, et un peu foiré l'arabe ) .

EDIT : pas vu ta réponse, sinon, ouép bien sûr y aura des exemples .

[Lostounet]

Merci Olympus :)
J'ai tout compris, à part un petit peu la loi de Morgan (je ne vois pas l'utilité O_o).
Cette proposition me pose problème: "Du faux suit le vrai" O_o
Sur ce, je te remercie de m'avoir accordé du temps de tes révisions ;D
Et surtout, bonne chance..!

Pour tes posts bene, je ne vois pas trop comment faire.. lol

[benekire2]

salut lostounet !

Je n'ai posté que deux "exercices"

Le premier : Trouver l'erreur :
|x|<1 <=> -1 -1-x<0<1-x <=> -1-x<1-x <=> -1<1

Le deuxième c'est rédiger proprement le truc que j'avais demandé :zen:

Mais tout le monde ( étudiants exclus ) peut jouer ( et c'est d'ailleur ça que j'attends ... )


Donc où c'est que tu plante ?
Si c'est là ... a part te donner la réponse je vois pas comment t'aider a part de te dire de regarder avec les deux yeux :id: ( c'est pas du tout méchant, c'est simplement que on peut buter une heure dessus ...)

Si c'est la deuxième, j'accepte (mais seulement pour toi) la preuve "laide" , pour être sur que tu as su le faire, sous réserve que tu me la rende correcte après !

[Olympus]

@benekire2 : pour ton premier, dis aussi "donc par équivalences successives, on a |x| < 1 <=> -1 < 1 , or -1 < 1 est toujours vraie, donc |x|<1 est aussi toujours vraie" ^^