Bonjour, j'ai un DM sur les produits scalaire à rendre pour mardi prochain. Il faut répondre par VRAI ou FAUX en justifiant la réponse.
Dans tout l'exercice, ABC est un triangle tel que AB=7 , AC=5 et BC=8.
On note I le milieu de [BC].
1)
a) On peut écrire AB.AC = (AB²+AC²-BC²)/2
b) AB.AC = -5
c) La valeur approchée par défaut de l'angle BAC à un degré près est 82°.
2) Soit (L1) l'ensemble des points tels que MA.AB = -5
a) C appartient à (L1)
b) M appartient à (L1) si et seulement si MC.AB = 0
c) (L1) est un cercle de diamètre [AB]
3) Soit (L2) l'ensemble des points tels que MB.MC = -7
a) On peut montrer, à l'aide de la relation de Chasles, que : MB.MC = MI²+(BC²)/2
b) M appartient à (L2) si et seulement si MI²=9
c) (L2) est un cercle de centre I et de rayon 3.
4) On se place dans un repère orthonormé (A, I, J) tel que : B(7;0) et C (xc;yc).
a) xc = AC*cosBAC = 5/7
b) C appartient au cercle de centre B et de rayon 8 donc yc = (20V3)/7
c) L'équation du cercle de diamètre [BC] est : x² + y² - (54x)/7 - (20V3)y/7 + 5 = 0.
Voici où j'en suis :
1)
a) Vrai
b) Faux : AB.AC = 5
c) Vrai : cosBAC = (AB.AC)/AB*AC) = 82°
Voilà, à partir de la question 2 je n'ai pas compris... Et je ne sais pas comment justifier la 1)a). Merci !
Produit scalaire
5 messages
- Page 1 sur 1
Re: Produit scalaire
Salut !
Qu'est-ce que tu ne comprends pas ?
2.a) Là il ne s'agit même pas de maths, il s'agit de français : appartient à
appartient à ) si et seulement si il vérifie l'équation
si et seulement si il vérifie l'équation  , c'est-à-dire si et seulement si
, c'est-à-dire si et seulement si  .
.
2.b) Utilise le fait que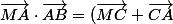\cdot \vec{AB}) puis développe.
puis développe.
2.c) La question précédente te donne la réponse.

GabrielCZ13 a écrit:à partir de la question 2 je n'ai pas compris
Qu'est-ce que tu ne comprends pas ?
GabrielCZ13 a écrit:2) Soit (L1) l'ensemble des points tels que MA.AB = -5
a) C appartient à (L1)
b) M appartient à (L1) si et seulement si MC.AB = 0
c) (L1) est un cercle de diamètre [AB]
2.a) Là il ne s'agit même pas de maths, il s'agit de français :
2.b) Utilise le fait que
2.c) La question précédente te donne la réponse.

- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Produit scalaire
Merci, donc la 2a et la 2b sont justes (je trouve -5). Par contre, la 2c est fausse car si MC.AB=0, cela suppose que AC.AB=0 or AC.AB = 5. Donc l'affirmation est fausse.
La 3a elle est fausse, ou alors je ne suis pas parvenu à trouver que MB.MC = MI² + BC²/2
car j'ai trouvé MI² + MI.BC + BC²/4
La 3a elle est fausse, ou alors je ne suis pas parvenu à trouver que MB.MC = MI² + BC²/2
car j'ai trouvé MI² + MI.BC + BC²/4
Re: Produit scalaire
bonjour
3/
MB.MC= (MI+IB).(MI+IC) = MI.MI + MI.(IB + IC) + IB.IC
avec IB+IC= 0
IB = - IC = BC/2
MB.MC = MI² - (BC/2)²
......
3/
MB.MC= (MI+IB).(MI+IC) = MI.MI + MI.(IB + IC) + IB.IC
avec IB+IC= 0
IB = - IC = BC/2
MB.MC = MI² - (BC/2)²
......
Re: Produit scalaire
Suis-je bête xD Merci !
La 3a est fausse
La 3b est juste, il suffit juste de remplacer BC par 8 dans le résultat de la 3a et on trouve MI²=9
La 3c est juste car : M appartient à L2 <--> MI²=9 <--> MI=3.
La 4a est juste car AC*cosBAC = 5*5/35 = 5/7
La 4b est juste car R²=(x-xb)²+(y-yb)² <--> 64 = (1936/49) + y² <--> y = 20V3/7
Et c'est bon, je sais comment faire pour la 4c. Merci beaucoup !!! Au revoir.
La 3a est fausse
La 3b est juste, il suffit juste de remplacer BC par 8 dans le résultat de la 3a et on trouve MI²=9
La 3c est juste car : M appartient à L2 <--> MI²=9 <--> MI=3.
La 4a est juste car AC*cosBAC = 5*5/35 = 5/7
La 4b est juste car R²=(x-xb)²+(y-yb)² <--> 64 = (1936/49) + y² <--> y = 20V3/7
Et c'est bon, je sais comment faire pour la 4c. Merci beaucoup !!! Au revoir.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
