Produit Scalaire DM

[marie72300]

j'ai besoin d'aide pour l'exercice suivant svp

l'énoncé est :
ABC est un triangle, ABDE et ACFG sont deux carrés:
1a) Démontrer que /vec{AE}./vec{AG} = /vec{-AB}./vec{AC}
b) Sachant que /vec{EC} = /vec{AC} -(moins) /vec{AE} et que /vec{BG} = /vec{AG} -(moins) /vec{AB}, démontrer que (EC) et (BG) sont perpendiculaires.
2a) Démontrer que /vec{AE}./vec{AC} = /vec{AB}./vec{AG}
b) En tenant compte de la décomposition des vecteurs /vec{EC} et /vec{BG} de la question 1b), démontrer que EC=BG
3) On note O le milieu de [EG] Démontrer que 2/vec{AO} = /vec{AE} +(plus) /vec{AG}
4) Démontrer que 2/vec{AO}./vec{BC} = 2/vec{AO}.(/vec{AC} -(moins) /vec{AB})
b) Démontrer que les droites (AO) et (BC) sont perpendiculaires

[capitaine nuggets]

j'ai besoin d'aide pour l'exercice suivant svp

l'énoncé est :
ABC est un triangle, ABDE et ACFG sont deux carrés:
1a) Démontrer que /vec{AE}./vec{AG} = /vec{-AB}./vec{AC}
b) Sachant que /vec{EC} = /vec{AC} -(moins) /vec{AE} et que /vec{BG} = /vec{AG} -(moins) /vec{AB}, démontrer que (EC) et (BG) sont perpendiculaires.
2a) Démontrer que /vec{AE}./vec{AC} = /vec{AB}./vec{AG}
b) En tenant compte de la décomposition des vecteurs /vec{EC} et /vec{BG} de la question 1b), démontrer que EC=BG
3) On note O le milieu de [EG] Démontrer que 2/vec{AO} = /vec{AE} +(plus) /vec{AG}
4) Démontrer que 2/vec{AO}./vec{BC} = 2/vec{AO}.(/vec{AC} -(moins) /vec{AB})
b) Démontrer que les droites (AO) et (BC) sont perpendiculaires

Salut, sur quelles question bloques-tu ?

[marie72300]

Salut, sur quelles question bloques-tu ?

Des la premiere question

[mathelot]

je peux te filer un de mes cours, le produit scalaire est bien expliqué
(et pour cause, je me suis inspiré du manuel Terracher de Term S)
ici

rubrique: Géométrie: produit scalaire

[capitaine nuggets]

1. Utilise une des définition du produit scalaire :
.
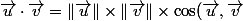Montrer cette égalité reviendra en fait à montrer une égalité de cosinus d'angles :++: