[ exo ] produit scalaire

[haricot29]

Bonjour tout le monde alors voila je suis en train de faire le produit scalaire, voila un exo sur lequel je bloque ( j'aime pas trop les barycentres Grrrr ça date !! ) Voila l'énoncé si quelqu'un pouvait me donner un petit coup de main s'il vous plait MERCI

ABCD est un carré de coté 1 et de centre O.

1/ a/ Construire le point G barycentre de (A;2) (B;1) (C;1)
b/ Soit le vecteur U est égal à -2MA + MB + MC ( ce sont des vecteurs).
Démontrer que le vecteur U est indépendant du point M.
Construire AA' (vecteur ) tel que AA' (vecteur) = AG ( pas vecteur ).

2/ Soit E l'ensemble de points du plan tels que : 2MA² - MB² - Mc² = 1.
a/ Exprimer 2MA² - MC² - MB² en fonction de AA' et AM ( vecteurs ).
b/ Déterminer et construire E.

3/ Soit F l'ensemble des points tel que 2 MA² + MB² + MC² = 6.
a/ Exprimer 2MA² + MC² + MB² en fonction de MG.
b/ Déterminer et construire F.

4/ Dans le repere orthonormal ( A ; AB ; AD ) ( vecteurs )
a/ Determner une équation cartésienne de E puis caractériser géométriquement E.
b/ Derterminer une équation cartésienne de F puis caractériser géométriquement F.

[Touriste]

Bonjour,

As-tu fait des choses ?

[haricot29]

ben euh :doh: a vrai dire j'ai contruit mon carré et construit mon barycentre lol je sias je n'ai rien fait mais je n'arrive pas a travailler abec les points abstraits tel que M ; pck pour ce qui des exos pour trouver des équations de droite et de cercle j'arrive niquel dc :mur:

[Touriste]

OK donc tu as fait le 1a.
Peux-tu répondre à la question suivante : quand est-ce que le barycentre des points pondérés (A,a), (B,b) et (C,c) existe ?

[haricot29]

il existe lorsque a + b + c différent de 0 ?! non :doh:

[Touriste]

Exact ! Et quand a+b+c=0, que peut-on dire du vecteur ?

[haricot29]

a Ma + b MB + C MC est alors nul

[Touriste]

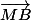
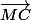
NON ! Dans la relation , applique la relation de Chasles en coupant et par A et dis-moi ce que tu obtiens.

[haricot29]

( quand c'est en majuscules ce sont des vecteurs )
a MA + b MA + AB + c MA + AC
= a+b+c MA + AB + AC ?! non ?!

[Touriste]

( quand c'est en majuscules ce sont des vecteurs )
a MA + b MA + AB + c MA + AC
= a+b+c MA + AB + AC ?! non ?!

Tu as oublié des parenthèses :
a MA + b (MA + AB) + c (MA + AC)
= (a+b+c) MA + bAB + cAC
= bAB + cAC
Ce sont des vecteurs partout (j'ai pris ta convention).
Tu vois donc que le vecteur aMA + bMB + cMC est indépendant de M...

Tu as ainsi la réponse au début de la question 1b. Il y a une erreur dans la suite de la question. Peux-tu corriger stp ?

[haricot29]

merci pour le 1/ b/
correction de la question :
Construire le point A' tel que AA' (vecteur) = U ( vecteur) . Calculer AA' ( vecteur) et AG ( pas vecteur ).

[Touriste]

AA' (vecteur) = AG ( pas vecteur ).

Cette égalité n'a pas de sens !
Est-ce que ce ne serait pas plutôt : construire A' tel que ?

[haricot29]

oui c'est cela j'ai recorriger dsl !
:id:

[Touriste]

OK. Dans les calculs précédents, on a donné une expression de indépendante du point M. Du coup la construction de A' ne doit pas te poser trop de problème...

[haricot29]

cela veut dire que le vecteur U équivaut a la diagonale AC et que le point A' et le meme que C ?!

[Touriste]

Non. On a montré que aMA+bMB+cMC=bAB+AC (vecteurs partout) dans le cas où a+b+c=0. Que valent ici a, b et c ?

[haricot29]

a = -2 ; b et c = 1
a + b +c = 0
donc U = AB + AC Soit AC non ?!

[Touriste]

a = -2 ; b et c = 1
a + b +c = 0
donc U = AB + AC

Jusque là OK.

Soit AC non ?!

Ben non ! Qu'utilises-tu pour trouver AC ?

[haricot29]

:mur: En me relisant c'est claire que je dis nimporte quoi j'ai confondu Ac avec AB !!! Pffff quel gignole
Donc c'est bon j'ai placer mon point A'

[haricot29]

pour calculer AA' je calcul AB puis AC et j'additionne
AB = 1 ( coté du carré)
AC est l'hypothénus de ABC
AC² = AB² + AC² = 2
AC = rac(2)
Donc AA' = 1 + rac(2) ??!!

et pour AG ?! :doh: