Exo produit scalaire 1èS

[Alice1S]

Bonjour, je viens de commencer le produit scalaire et je n'ai pas tout compri, j'ai donc du mal à faire cet exercice. J'attends votre aide :). Je vous donne tout l'énnoncé.

ABCD est un carré de côté de 4cm. I et J sont définis par les relations : AI=1/3AD et BJ=3/4BC.

1°) On pose u=1/4AB et v=1/4AD

Justifier que le repère (A;u;v) est orthonormal.

(Je voudrai trouver les coordonnées de u et v pr faire la formule : xx'+yy'= 0. Bonne idée ?!)

2°) Quelles sont les coordonnées dans ce repère des points A, B, C, D, I et J ?

3°) Calculer alors les pdts scalaires : AB.AC et AD.IJ .

4°) Soit M un point de la droite (CD), défini par la relation : DM= x DC
Quelles sont les coordonnées de M dans le repère (A;u;v) ?
Déterminer alors la position du point M pour que la droite (BM) soit perpendiculaire à la droite (IJ).

Merci d'avance. :lol3:

[Arnaud-29-31]

Salut Alice,

Trouver les coordonnées de et ? Dans quel repère ? ^^
Pour la question 1 il faut juste montrer qu'ils sont orthogonaux grâce aux propriétés du carré puis de même norme et on pourra dire que le repère est orthonormé.

Je te laisse chercher la suite, les coordonnées des points ca ne doit pas être trop dur.

[Alice1S]

Propriété du carré ?! :doh:

[Arnaud-29-31]

Bein oui ... dans un carré, il y a des angles droits ...
et étant respectivement colinéaires à et , c'est pas très dur de montrer que est orthogonal à

[Alice1S]

Ah oui ! Ok ! j'étais partie ds une relation pr le pdt scalaire :--: ! Merci.
J'aurai p-e (surement !! ><) d'autres questions plus tard..

[Alice1S]

Bonjour je trouve :
2) A(0;0) B(1;0) C(1;1) D(0;1) I(0;1/3) et J (1;3/4)

3) AB.AC
AB(1;0) AC(1;1)
lamba/2=xx'+yy' = 1+0 = 1

AD.IJ
AD(0;1) IJ(1;5/12)
lamba/2=5/12

J'ai bon ? (Des ami(e)s ne trouvent pas la même chose que moi. Certains trouvent : 16 et 20/3 , d'autres 22 et 149/9)

[XENSECP]

Bonjour je trouve :
2) A(0;0) B(1;0) C(1;1) D(0;1) I(0;1/3) et J (1;3/4)

Non.

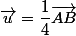
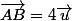
Si alors donc c'est plutôt B(4;0).

Je te laisse revoir les autres points

[Alice1S]

en fait j'me ss plantée g fait ds le repère A, AB, AD et non A,u,v !

[Alice1S]

Par contre je reste bloquée sur la question 4 :S ..

[Arnaud-29-31]

Tu a commencé comment ? Montre nous ce que tu as fait

[XENSECP]

donc tu peux connaître les coordonnées de M en fonction des coordonnées de D et C (que tu as) et de x (l'inconnue).

Revoit ton cours

[Alice1S]

Oui, j'ai trouvé les coordonnées de DC ms après je ne sias pas cmt avancer.

Je commence tout juste le produit scalaire, je n'ai pas énormémeent de cours ... !!!!!

[XENSECP]

Je commence tout juste le produit scalaire, je n'ai pas énormémeent de cours ... !!!!!

ca n'a rien à voir avec le produit scalaire... c'est juste une histoire de coordonnées.

[Arnaud-29-31]

Bon, on est d'accord que A(0,0) B(4,0) C(4,4) D(0,4) I(0,) et J(4,3) ?
Tu as trouvé quoi pour les coordonnées de M ?

[Alice1S]

J'ss Ok pour les points.
Je n'ai rien pour M, je ne vois pas quoi appliquer/utiliser

[Arnaud-29-31]

Bein il est sur DC donc déjà tu connais son ordonnée ... pour l'abscisse on sait que DM = x.DC ... donc ?

[Alice1S]

DC (4;0)
DM = x DC
xM-xD = x(xC-xD)
yM-yD = x(yC-yD)

xM=4x yM=4

M(4x;4)

[XENSECP]

DC (4;0)
DM = x DC
xM-xD = x(xC-xD)
yM-yD = x(yC-yD)

xM=4x yM=4

M(4x;4)

T'es sure d'avoir bien résolu les équations ?

[Alice1S]

Mmmmh oui :/

[XENSECP]

Alors c'est bon... ^^

Déterminer alors la position du point M pour que la droite (BM) soit perpendiculaire à la droite (IJ).

Reste plus qu'à trouver x qui vérifie ça